Vorlesungsskriptum

Lineare Algebra I

Themenüberblick:

• Vektorrechnung: Linearkombination, linear (un)abhängig, Dimension, (Unter-)Vektorraum
• Vektoren und Matrizen in linearen Gleichungssystemen
• lineare Funktionen: inneres Produkt, Transponieren, Gradient, Transformation vom Inputraum in den Outputraum, Konturlinien

Code

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D

Code

plt.rcParams['figure.figsize']=(4,4)

Vektorrechnung

Notation(en) und erste Begriffe:

Ein Vektor mit \(n\) Komponenten (auch Elemente oder Koordinaten genannt), ein sogenannter \(n\)-Vektor, wird typischer Weise als Spaltenvektor

\[\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}\]

oder Zeilenvektor

\[(x_1, x_2, \ldots , x_n)\]

geschrieben.

Transponieren, geschrieben mit einem hochgestellten \(T\), macht einen Spaltenvektor zum Zeilenvektor und umgekehrt:

\[\begin{align} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}^T & = (x_1, x_2, \ldots , x_n), \\ (x_1, x_2, \ldots , x_n)^T & = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}. \end{align}\]

Gibt man einem Vektor z. B. den Namen \(x\), so heißt \(x^T\) der transponierte Vektor, und es gilt offenbar \((x^T)^T = x\). Die Unterscheidung in Spalten- und Zeilenvektoren ist erst in der Matrizenrechnung relevant und man könnte in der reinen Vektorrechnung einen \(n\)-Vektor einfach(er) als eine geordnete Liste von \(n\) Zahlen definieren. Wir werden aber die Vorzüge der Matrixmultiplikation und des Transponierens von Beginn an verwenden und Vektoren als Spalten- oder Zeilenvektoren schreiben. Diese identifizieren wir für die Matrizenrechnung mit \(n\times 1\) bzw. \(1\times n\) Matrizen.

Anwendungen und graphische Darstellungen von Vektoren:

Vektoren werden zur Modellierung von sehr vielen Objekten verwendet. Hier die bekanntesten:

• Punkte: in der Ebene und im Raum, Ereignisse in der Raumzeit, etc.
• Pfeile: Ortsvektor, Verschiebung, Geschwindigkeit, Beschleunigung, Kraft, (Dreh-)Impuls etc.
• (technische) Signale und andere Zeitreihen wie z. B. cash flows
• Listen: Preisvektor, Einkaufskorb, Allokation etc.

Die lineare Struktur eines Vektorraums:

Die folgenden zwei Rechenoperationen definieren auf einer Menge einen Vektorraum:

• Skalarmultiplikation: Die elementweise Multiplikation eines Skalars (einer Zahl) mit allen Vektorkomponenten liefert wieder einen Vektor. \(\rightarrow \lambda \cdot \begin{pmatrix} x_1\\ x_2 \\ x_3\end{pmatrix} = \begin{pmatrix} \lambda \cdot x_1 \\ \lambda \cdot x_2 \\ \lambda \cdot x_3\end{pmatrix}\)

• Addition: elementweise, liefert wieder einen Vektor \(\rightarrow \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} + \begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix} = \begin{pmatrix} x_1+y_1 \\ x_2+y_2 \\ x_3+y_3 \end{pmatrix}\)

Es gelten die üblichen, intuitiven Rechenregeln. Die Interpretation von Skalarmultiplikation und Addition hängt davon ab, was die Vektoren modellieren.

Ein Ausdruck der Form \(\alpha x + \beta y\) mit \(\alpha, \beta \in \mathbb{R}\) und \(x, y \in \mathbb{R}^n\) oder allgemeiner \(\alpha_1 v_1 + \alpha_2 v_2 + \ldots + \alpha_k v_k\) mit \(\alpha_i \in \mathbb{R}\) und \(v_i \in \mathbb{R}^n\) heißt Linearkombination der vorkommenden zwei bzw. \(k\) Vektoren.

Lineare Abhängigkeit:

Eine Menge von \(k\) Vektoren \(v_1, v_2, \ldots, v_k\) heißt linear unabhängig, wenn die Gleichung \(\alpha_1 v_1 + \alpha_2 v_2 + \ldots + \alpha_n v_n = 0\) nur die triviale Lösung \(\alpha_i = 0\) hat. Andernfalls heißen die \(k\) Vektoren linear abhängig und mindestens einer der vorkommenden Vektoren läßt sich als Linearkombination der restlichen ausdrücken.

Das innere Produkt:

Eine weitere Rechenoperation stellt das innere Produkt (engl. inner product oder dot product) dar, das für zwei Spaltenvektoren \(x =\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}\) und \(y =\begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}\) durch Multiplizieren entsprechender Komponenten und anschließendes Aufsummieren eine Zahl liefert. Unter Verwendung der Matrizenmultiplikation schreiben wir das innere Produkt von \(x\) mit \(y\) als

\[x^Ty = (x_1, x_2, \ldots , x_n)\begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} = x_1 y_1 + x_2 y_2 + \ldots x_n y_n.\]

Es gilt \(x^T y = y^T x\).

Die Länge \(\lVert x\rVert\) (euklidische Norm) eines Vektors \(x\) ist über den verallgemeinerten Satz von Pythagoras als \(\lVert x\rVert = \sqrt{x_1^2 + x_2^2 + \ldots + x_n^2}\) definiert und kann mit Hilfe des inneren Produktes als \(\lVert x\rVert = \sqrt{x^T x}\) geschrieben werden.

Wenn wir den Winkel zwischen zwei Vektoren \(x\) auf \(y\) mit \(\varphi\) bezeichnen, so gilt: \[x^T y = \lVert x\rVert \lVert y\rVert \cos(\varphi).\]

Der Ausdruck \(\cos(\varphi)\) ergibt sich in dieser Formel aufgrund der orthogonalen Projektion des Vektors \(x\) auf den Vektor \(y\).

Lineare Funktionen

Definierende Eigenschaften:

Eine lineare Funktion von \(\mathbb{R}^n\) nach \(\mathbb{R}\) ist gegeben durch das innere Produkt eines fixen Vektors \(c\) mit einem variablen Vektor \(x\):

\[f(x) = c^T x = c_1 x_1 + c_2 x_2 + \ldots + c_n x_n.\]

Jede lineare Funktion erfüllt die Linearitätseigenschaft

\[f(\alpha x + \beta y) = \alpha f(x) + \beta f(y),\]

und jede Funktion, die die Linearitätseigenschaft erfüllt, ist von der Form \(f(x) = c^Tx\).

Geometrische Darstellung:

• Die Konturlinien einer linearen Funktion in der Ebene sind parallele Geraden, und die Null-Konturlinie geht durch den Ursprung.
• Die Konturflächen einer linearen Funktion im Raum sind parallele Ebenen, und die Null-Konturfläche geht durch den Ursprung.

Der Koeffizientenvektor \(c\) der linearen Funktion \(f(x) = c^Tx\)

• ist orthogonal (=rechtwinklig) zu den Konturlinien bzw. Konturflächen.
• zeigt in Richtung steigender Funktionswerte der linearen Funktion.

Beispiel: Konturplot

Konturplot der linearen Funktion

\[f:\mathbb{R}^2 \rightarrow \mathbb{R}: f(x) = -2x_1 + 3x_2.\]

Der Koeffizientenvektor ist \(c = \begin{pmatrix} -2 \\ 3 \end{pmatrix}\), d. h. \(f(x) = c^T x\).

Code

delta = 0.25
x1 = np.arange(-5.0, 5.0, delta)
x2 = np.arange(-5.0, 5.0, delta)
X1, X2 = np.meshgrid(x1, x2)

c = np.array([-2, 3])
Y = c[0]*X1 + c[1]*X2

plt.figure()
plt.axis('equal')
plt.arrow(0, 0, c[0], c[1], head_width=0.1, fc='k', linewidth=1)
CS = plt.contour(X1, X2, Y, levels= np.arange(-20, 30, 5), cmap='coolwarm_r')
plt.clabel(CS, inline=1, fmt='%1.1f')
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.grid(True)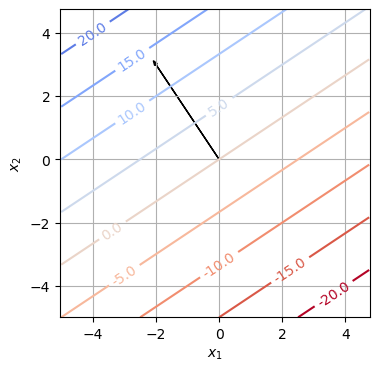

Lineare Algebra II

Themenüberblick:

• Rechenregeln der Matrizenrechnung: Transponieren, Matrixmultiplikation, Addition, Skalarmultiplikation, spezielle Matrizen
• lineare Funktionen: Inputraum -> Outputraum, Drehungen etc.
• lineare Gleichungssysteme: Geometrie, Formulierung als lineare Funktion(en) (Zeilen- und Spaltensicht), Lösungsstruktur (Eindeutigkeit und Existenz), inverse Matrix, Determinante, Rang einer Matrix
• Eigenwerte und -vektoren: evtl. als Programmierprojekt

Rechnen mit Matrizen

Spalten- und Zeilenansicht von Matrizen:

Eine Matrix kann auf folgende Arten gesehen werden:

• als Stapel von Zeilenvektoren
• als Stapel von Spaltenvektoren
• als 2-dimensionale Anordnung von Zahlen

Zahlen und Vektoren als Matrizen:

• Zahl: \(1\times 1\)-Matrix
• Zeilenvektor: \(1\times n\)-Matrix
• Spaltenvektor: \(n\times 1\)-Matrix

Matrixprodukt:

Das Matrixprodukt einer \(n\times m\)-Matrix mit einer \(m\times p\)-Matrix liefert eine \(n\times p\)-Matrix. Die innere Dimension muß übereinstimmen, hier ist sie \(m\). Das Ergebnis hat die äußeren Dimensionen, hier \(n\) und \(p\).

Produkttypen:

• Zeilenvektor \(\times\) Spaltenvektor = Zahl
• Matrix \(\times\) Spaltenvektor = Spaltenvektor
• Zeilenvektor \(\times\) Matrix = Zeilenvektor
• Matrix \(\times\) Matrix = Matrix

spezielle Matrizen:

• Nullmatrix: enthält lauter Nullen, Notation \(0\)
• Einheitsmatrix: \(n\times n\)-Matrix (quadratisch), Einser auf der Diagonalen (=Elemente mit gleichem Zeilen- und Spaltenindex), ansonsten Nullen, Notation \(I\) oder \(\mathbb{1}\)
• Inverse Matrix: Zu einer quadratischen Matrix \(A\) kann (muss aber nicht) eine inverse Matrix, geschrieben als \(A^{-1}\), existieren. Sie entspricht dem Kehrwert für Matrizen und hat die Eigenschaften: \(A^{-1}A = I = AA^{-1}\).

Determinante:

Die Determinante ist eine Zahl, die nur für quadratische Matrizen (gleich viele Zeilen wie Spalten) berechnet werden kann. Notation \(\det(A)\) und \(\lvert A \rvert\)

Beispiel: \(A=\begin{pmatrix} 3 & 2 \\ -1 & 4\end{pmatrix}\) hat die Determinante \(\det(A) = 3\cdot 4 - (-1)\cdot 2 = 14\). Vergleiche die Berechnung des Kreuzproduktes von zwei räumlichen Vektoren.

Geometrie: Der Betrag der Determinante ist gleich dem Flächeninhalt (allg. dem Volumen) des von den Spaltenvektoren der Matrix aufgespannten Parallelepipeds.

Formeln:

• \(2\times 2\)-Matrizen: \(\det\begin{pmatrix} a & b \\ c & d\end{pmatrix} = ad - cb\). Für eine \(2\times 2\)-Matrix \(A=\begin{pmatrix} a & b \\ c & d\end{pmatrix}\) ist die inverse Matrix, falls \(\det(A)\neq 0\), durch \(A^{-1} = \frac{1}{\det(A)} \begin{pmatrix} d & -b \\ -c & a\end{pmatrix}\) gegeben.
• \(3\times 3\)-Matrizen: \(\det\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}= a_{11} a_{22} a_{33} +a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{22} a_{31} - a_{12} a_{21} a_{33} - a_{11} a_{23} a_{32}\)

Ist die Determinante einer Matrix = 0, so existiert zu dieser Matrix keine inverse Matrix und ein lineares Gleichungssystem mit der Matrix der Koeffizienten ist nicht eindeutig lösbar.

Lineare Funktionen

Definition:

Eine lineare Funktion \(f\) zwischen den Vektorräumen \(\mathbb{R}^n \rightarrow \mathbb{R}^m\) ordnet jedem Inputvektor \(x\in\mathbb{R}^n\) genau einen Outputvektor \(f(x) \in\mathbb{R}^m\) auf eine Weise zu, sodass die Linearitätseigenschaft

\[f(\alpha x + \beta y) = \alpha f(x) + \beta f(y)\]

für alle Zahlen \(\alpha\) und \(\beta\) und alle Inputvektoren \(x\) und \(y\) erfüllt ist.

Eigenschaften:

• Jede lineare Funktion läßt sich in Matrixform \(f(x) = Ax\) für eine eindeutige \(m\times n\)-Matrix \(A\) schreiben.
• Jede Funktion \(f(x)\), die sich in Matrixform \(f(x) = Ax\) schreiben läßt, ist linear.

Beispiele:

• Der Drehung in der Ebene um den Winkel \(\alpha\) gegen den Uhrzeigersinn entspricht die Drehmatrix \(R=\begin{pmatrix} \cos(\alpha) & -\sin(\alpha) \\ \sin(\alpha) & \cos(\alpha) \end{pmatrix}\).

• Der Spiegelung in der Ebene an der 1-Achse entspricht die Matrix \(S=\begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix}\).

Darstellung des Outputs:

• Der Outputvektor einer linearen Abblildung \(Ax\) kann als Linearkombination der Spalten von \(A\) dargestellt werden. Beispiel: \(Ax= \begin{pmatrix} 1 & 2 \\ 3 & 4\end{pmatrix}\begin{pmatrix} x_1 \\ x_2\end{pmatrix} = x_1\begin{pmatrix} 1 \\ 3\end{pmatrix} + x_2\begin{pmatrix} 2 \\ 4\end{pmatrix}.\)

• Der Outputvektor einer linearen Abblildung \(Ax\) kann als Spaltenvektor der linearen Funktionen der Zeilenvektoren von \(A\) dargestellt werden. Beispiel: \(Ax= \begin{pmatrix} 1 & 2 \\ 3 & 4\end{pmatrix}\begin{pmatrix} x_1 \\ x_2\end{pmatrix} = \begin{pmatrix} 1x_1 + 2x_2 \\ 3x_1 + 4x_2\end{pmatrix}.\)

Lineare Gleichungssysteme

Jedes lineare Gleichungssystem mit \(m\) Gleichungen und \(n\) Variablen kann in der Matrixform \(Ax=b\) geschrieben werden.

• \(A\) die \(m\times n\)-Matrix der Koeffizienten
• \(x\) der \(n\times 1\)-Spaltenvektor der Variablen
• \(b\) der \(m\times 1\)-Spaltenvektor der rechten Seite der Gleichung

Ein Vektor \(x\), der \(Ax=b\) erfüllt, ist eine Lösung des lineare Gleichungssystems. Ein Lösung ist somit ein Input der linearen Funktion \(Ax\), der den Output \(b\) hat.

Formtypen:

Ein Gleichungssystem ist von einem der drei folgenden Formtypen:

• quadratisch: \(m = n\), d. h. gleich viele Gleichungen wie Variablen
• überbestimmt: \(m > n\), d. h. mehr Gleichungen als Variablen
• unterbestimmt: \(m < n\), d. h. weniger Gleichungen als Variablen

Lösungsstruktur:

Ein Gleichungssystem hat entweder keine, eine oder unendlich Lösungen.

Lösungsmethoden und -kriterien:

Für alle Gleichungssysteme \(Ax=b\):

Gaußsches Eliminationsverfahren: geschickte Kombination von Äquivalenzumformungen des Gleichungssystems, d. h. Multiplizieren (außer mit Null), Vertauschen und Addieren von Gleichungen, liefert die Lösungsmenge, die leer ist, falls keine Lösung existiert.

Der Rang einer Matrix \(A\) ist die Anzahl linear unabhängiger Spalten- oder Zeilenvektoren der Matrix. Notation: \(\text{Rang}(A).\) Ein Gleichungssystem \(Ax=b\) habe eine \(m\times n\)-Koeffizientenmatrix \(A\) mit Rang \(r\), der sicher kleiner gleich \(m\) und \(n\) ist. Dann gilt:

• 1. Falls \(r=m\), dann existiert mindestens eine Lösung.
• 2. Falls \(r=n\), dann ist eine Lösung eindeutig.
• 3. Falls \(r=m=n\), dann existiert genau eine Lösung.

\((A|b)\) bezeichne die mit der zusätzlichen Spalte \(b\) erweiterte Koeffizientenmatrix. Dann gilt:

• 4. \(Ax=b\) ist genau dann lösbar, wenn \(\text{Rang}(A) = \text{Rang}(A|b)\).
• 5. \(Ax=b\) hat eine eindeutige Lösung, wenn \(\text{Rang}(A) = \text{Rang}(A|b) = n\).
• 6. \(Ax=b\) hat unendlich viele Lösungen, wenn \(\text{Rang}(A) = \text{Rang}(A|b) < n\).
• 7. \(Ax=b\) hat keine Lösung, wenn \(\text{Rang}(A) \neq \text{Rang}(A|b)\).

Überprüfen der Lösbarkeit eines linearen Gleichungssystems:

1. Ermittlung des Rangs der einfachen Koeffizientenmatrix \(\text{Rang}(A)\).
2. Ist \(\text{Rang}(A)\) gleich der Anzahl der Unbekannten \(n\), so ist das Gleichungssystem eindeutig lösbar.
3. Ist \(\text{Rang}(A)\) kleiner der Anzahl der Unbekannten \(n\), dann ist der Rang der erweiterten Koeffizientenmatrix \(\text{Rang}(A|b)\) zu ermitteln.
4. Gilt \(\text{Rang}(A) = \text{Rang}(A|b) < n\), dann gibt es unendlich Lösungen, ansonsten gibt es keine Lösung

Eigenwerte und -vektoren

Motivation:

Der Effekt einer linearen Abbildung, also die Multiplikation eines Vektors \(x\) mit einer Matrix \(A\), ist im Allgemeinen unübersichtlich, d. h. der Output \(Ax\) hängt vom Input auf eine komplizierte Weise ab. Wäre der Effekt eine reine Skalarmultiplikation \(\lambda x\), so wäre der Output eine Umsaklierung (Streckung, Stauchung, Umkehrung) des Inputs \(x\) und deutlich einfacher zu handhaben.

Anwendungen:

• Entkoppeln von Gleichungen: Dynamische Systeme, Differentialgleichungen (-> Eigenfrequenzen, etc.)
• Nicht-lineare Optimierung: Kriterium für lokales Maximum bzw. Minimum
• Hauptachsentransformation, Principal Component Analysis

Definition:

Ein Eigenvektor einer quadratischen Matrix \(A\) ist ein nicht-Null-Vektor \(x\), sodass

\[Ax = \lambda x\]

für eine Zahl \(\lambda\) gilt. Die Zahl \(\lambda\) ist der Eigenwert von \(A\) zum Eigenvektor \(x\).

Achtung: Jedes Vielfache eines Eigenvektors ist wieder Eigenvektor zum selben Eigenwert: \(A(\alpha x) = \alpha Ax = \alpha \lambda x = \lambda (\alpha x)\).

Berechnung:

Falls \(x\) ein Eigenvektor von \(A\) zum Eigenwert \(\lambda\) ist, dann gelten:

\[\begin{align} Ax & = \lambda x \\ Ax - \lambda x & = 0 \\ Ax - \lambda I x & = 0 \\ (A - \lambda I) x & = 0. \end{align}\]

Da \(x\) laut Annahme ein nicht-Null-Vektor ist, hat das letzte Gleichungssystem neben der trivialen Lösung des Nullvektors mit \(x\) eine zweite und somit nicht eindeutige Lösung. Daher muss die Determinante der Koeffizientenmatrix Null sein:

\[\det(A - \lambda I) = 0.\]

Andernfalls hätte das letzte Gleichungssystem eine eindeutige Lösung. Aus der Bedingung \(\det(A - \lambda I) = 0\) lassen sich alle Eigenwerte berechnen. Anschließend kann zu jedem Eigenwert \(\lambda\) ein Eigenvektor berechnet werden, indem eine nicht-triviale Lösung von \((A - \lambda) x = 0\) bestimmt wird.

Beispiele

Lineare Abbildung - Drehung: Drehen eines Vektors, der als Pfeil interpretiert wird:

Code

alpha = np.pi/4  # 45°
R = np.array([[np.cos(alpha), -np.sin(alpha)],
           [np.sin(alpha),  np.cos(alpha)]])
x = np.array([1, 1])
y = np.dot(R, x)

plt.figure()
plt.arrow(0, 0, x[0], x[1], head_width=.1, color='green')
plt.arrow(0, 0, y[0], y[1], head_width=.1, color='blue')
plt.xlim(-1,2)
plt.ylim(-1,2)
plt.grid(True)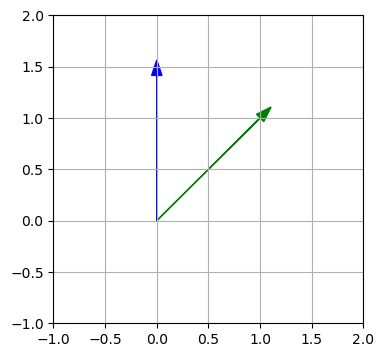

Regression

Themenüberblick:

• Problemstellung: Ausgleichsgerade, überbestimmtes Gleichungssystem, kleinste Fehlerquadratsumme
• Matrixformulierung: OLS-Fit und -Formel
• Geometrie: orthogonale Projektion, Eindeutigkeit der Lösung
• Anwendungen: Prognose, polynomialer Fit, Transformationen, allgemeine quadratische Zielfunktionen, Lösen von Gleichungssystemen

Problemstellung

Beispiel: Ausgleichsgerade

Wir beginnen mit dem klassischen Beispiel des Fits einer Geraden durch \(n\) Datenpunkte.

Code

n = 13                       # number of data points
t = np.linspace(1, 10, num = n) # time points measurements
noise = 0.4*np.random.randn(n)         # noise in measurement values 
y = 2 + 0.5*t + noise        # measurement values: line + noise 

plt.figure()
plt.plot(t, y, 'o')
plt.xlabel('t')
plt.ylabel('y')
plt.grid(True)

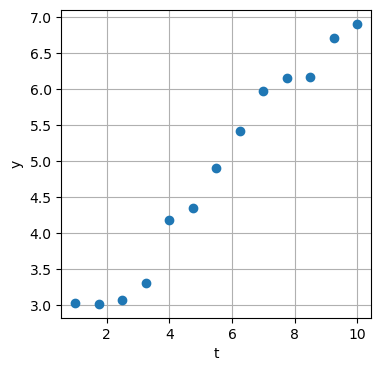
Ziel: Fit einer Geraden \(y(t) = d + kt\) durch die Datenpunkte \((t_i,y_i)\), sodass der “Fehler”, der noch zu definieren ist, klein ist. In anderen Worten: Finde die “optimalen” Werte für \(d\) und \(k\) aus den Datenpunkten.

Vorgehensweise: Wir formulieren das lineare Gleichungssystem

\[\begin{align} d + kt_1 & = y_1 \\ d + kt_2 & = y_2 \\ \vdots & = \vdots \\ d + kt_n & = y_n \end{align}\]

für die zwei unbekannten Größen \(d\) und \(k\) als Matrixgleichung \(Ax=b\):

\[\begin{pmatrix} 1 & t_1 \\ 1 & t_2 \\ \vdots & \vdots \\ 1 & t_n \end{pmatrix} \begin{pmatrix} d \\ k \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}.\]

Das lineare Gleichungssystem ist typischer Weise nicht lösbar, da meist keine Gerade durch alle Datenpunkte legbar ist. Stattdessen soll der Fehler minimiert werden. Wir definieren als \(i\)-ten Einzelfehler \(e_i\) die \(y\)-Differenz zwischen dem Fit \(\hat{y}_i := d + kt_i\) und dem zugehörigen Datenwert \(y_i\), d. h., \(e_i = d + kt_i - y_i\). Der Fehlervektor \(e\) besteht aus allen \(n\) Einzelfehlern. In Matrixnotation lässt er sich leicht durch \(e = Ax - b\) berechnen. Wir verlangen, dass der Fehlervektor minimale Länge haben soll. Das heißt \(\lVert e \rVert = \sqrt{e_1^2 + e_2^2 + \ldots + e_n^2}\) soll minimal sein, was äquivalent ist zu \(\lVert e \rVert^2 = e_1^2 + e_2^2 + \ldots + e_n^2\) soll minimal sein. In Matrixnotation: \(\lVert e \rVert = \lVert Ax - b \rVert\). Diese Vorgehensweise heißt Methode der kleinsten Fehlerquadrate, andere Bezeichnungen sind Regression und least squares.

Matrixformulierung

Formulierung des allgemeinen Optimierungsproblems:

Das obige Optimierungsproblem läßt sich in Matrixform schreiben als

\[\text{min. } \lVert Ax - b \rVert.\]

Umgekehrt wird jedes Optimierungsproblem, das sich als \(\text{min. } \lVert Ax - b \rVert\) schreiben läßt auch als Regressionsproblem bezeichnet.

Hinweis: Die Probleme \(\text{min. } \lVert Ax - b \rVert\) und \(\text{min. } \lVert Ax - b \rVert^2\) sind äquivalent.

Lösung in Matrixform:

Falls der Rang der Matrix \(A\) maximal ist, dann hat das Regressionsproblem die eindeutige Lösung

\[\hat{x} = (A^T A)^{-1}A^T b.\]

Der optimale Vektor \(\hat{x}\) ist auch Lösung des Gleichungssystems

\[A^T A \hat{x} = A^T b.\]

Die Gleichungen dieses Gleichungssystems heißen Normalgleichungen.

Lösungsvarianten in Python:

• über die Formel \(\hat{x} = (A^T A)^{-1}A^T b\)
• Lösen der Normalgleichungen mit solve
• mit dem Befehl lstsq

Code

col_of_ones = np.ones(n)
A = np.stack((col_of_ones, t), axis=1)
b = y.reshape(13,1)

# print(A)
# print(b)

Code

# via Formel
x_hat_1 = np.linalg.inv(A.T @ A) @ A.T @ b
print(x_hat_1)

# via Normalgleichungen
x_hat_2 = np.linalg.solve(A.T @ A, A.T @ b)
print(x_hat_2)

# via lstsq
x_hat_3 = np.linalg.lstsq(A, b, rcond=None)[0]
print(x_hat_3)

[[2.15065544]
 [0.49347604]]
[[2.15065544]
 [0.49347604]]
[[2.15065544]
 [0.49347604]]

Code

# Fit A*x_hat:
y_hat = A @ x_hat_1     # same as y_hat = x_hat_1[0] + x_hat_1[1]*t 

plt.figure()
plt.plot(t, y, 'o', label='data')
plt.plot(t, y_hat, 'o-', label='fit')
plt.xlabel('t')
plt.ylabel('y')
plt.legend(loc='best')
plt.grid(True)

Anwendungen

Prognose:

Regressionen werden sehr oft für Prognosen verwendet: Die Spalten der \(n\times m\) Matrix \(A\) bilden dabei die jeweils \(n\) historischen Werte der \(m\) erklärenden Größen. Nach dem Fit an die \(n\) historischen Werte \(b\) der zu erklärenden Größe stehen die optimalen Koeffizienten im Vektor \(\hat{x}\) zur Verfügung. Damit können neue Werte der zu erklärenden Größe berechnet werden, indem die zugehörigen neuen Werte der \(m\) erklärenden Größen mit den Koeffizienten des Vektors \(\hat{x}\) multipliziert werden.

Code

t_new = np.array([11, 12, 13])
col_of_ones_new = np.ones(3)
A_new = np.stack((col_of_ones_new, t_new), axis=1)
y_new = A_new @ x_hat_1    # same as y_new = x_hat_1[0] + x_hat_1[1]*t_new

Code

plt.figure()
plt.plot(t, y, 'o', label='data')
plt.plot(t_new, y_new, 'o-', label='forecast')
plt.xlabel('t')
plt.ylabel('y')
plt.legend(loc='best')
plt.grid(True)

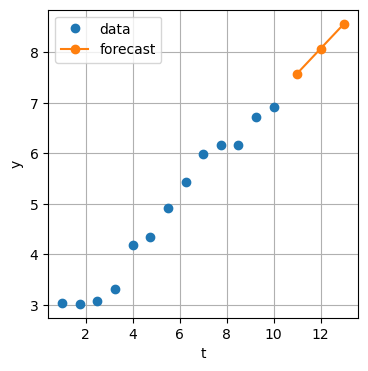
Polynomialer Fit:

Verallgemeinerung der Ausgleichsgerade als Polynom 1. Ordnung auf z. B. Polynome 3. Ordnung mit gesuchten Koeffizienten \(c_0\), \(c_1\), \(c_2\) und \(c_3\):

\[\begin{align} c_0 + c_1 t_1 + c_2 t_1^2 + c_3 t_1^3 & = y_1 \\ c_0 + c_1 t_2 + c_2 t_2^2 + c_3 t_2^3 & = y_2 \\ \vdots & = \vdots \\ c_0 + c_1 t_n + c_2 t_n^2 + c_3 t_n^3 & = y_n \end{align}\]

als Matrixgleichung \(Ax=b\):

\[\begin{pmatrix} 1 & t_1 & t_1^2 & t_1^3 \\ 1 & t_2 & t_2^2 & t_2^3 \\ \vdots & \vdots \\ 1 & t_n & t_n^2 & t_n^3 \end{pmatrix} \begin{pmatrix} c_0 \\ c_1 \\ c_2 \\c_3 \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}\]

Die optimalen Koeffizienten sind Lösung des Regressionsproblems \(\text{min. } \lVert Ax - b \rVert\).

Transformationen:

Beispiel: Das exponentielle Wachstumsmodell

\[n(t) = \alpha^{t - t_0}\]

mit unbekannten Parametern \(\alpha\) und \(t_0\) kann durch Logarithmieren zu einem linearen Modell

\[\begin{align} \log(n(t)) & = (t - t_0) \log(\alpha) \\ \log(n(t)) & = -t_0 \log(\alpha) + \log(\alpha)t \end{align}\]

transformiert werden. Das resultierende lineare Modell kann als Ausgleichsgerade mittels Regression behandelt werden. Dabei entspricht \(d=-t_0 \log(\alpha)\) und \(k=\log(\alpha)\).

Mehrdimensionale Differentialrechnung

Themenüberblick:

• Einführung: differentiale Größen, Auswahl an Anwendungen
• lineare Approximation von Funktionen: erste Ableitung, partielle Ableitung, Gradient, (totales) Differential
• Rechnen mit Differentialen: Jacobimatrix, Kettenregel

Einführung

Differentiale Größen:

Oft ist nicht (nur) der Wert einer Größe \(y\) interessant sondern seine Änderung im Verhältnis zur Änderung einer anderen Größe \(x\). Man arbeitet dann mit Begriffen wie (Änderungs-)Rate, Preis, Steigung, spezifische Größe, (z. B. Wärme-)Kapazität, Ableitung, partielle Ableitung, totale Ableitung, Differential, Gradient, etc.

Mathematisch wird die Abhängigkeit einer Größe \(y\) von einer Größe \(x\) als Funktion \(y = f(x)\), oder kurz \(y(x)\), beschrieben. Hängt \(y\) von \(n\) anderen Größen \(x_1, x_2, \ldots , x_n\) ab, dann betrachtet man eine Funktion \(y = f(x_1, x_2, \ldots , x_n),\) oder kurz \(y(x_1, x_2, \ldots , x_n)\). Die Berechnung und Verwendung der Änderung von \(y\) pro Änderung von \(x\) bzw. \(x_k\) ist das Gebiet der eindimensionalen bzw. mehrdimensionalen Differentialrechnung.

Auswahl an Anwendungen:

• lineare Approximation nicht-linearer Funktionen
• Taylorreihe: Verallgemeinerung zu polynomialer Approximation nicht-linearer Funktionen
• Optimalitätsbedingungen für nicht-lineare Optimierung
• kontinuierliche, (nicht-)lineare dynamische Systeme: gewöhnliche und partielle Differentialgleichungen
• Physik, Chemie, Technik: Mechanik, Thermodynamik, Elektrodynamik etc.
• Lösen nicht-linearer Gleichungen und Gleichungssysteme
• Variationsrechnung, Theorie der optimalen Steuerungen

Lineare Approximation von Funktionen

Achtung: Genau genommen wird nicht die Funktion linear approximiert sondern die Änderung der Funktion bei einem bestimmten Inputwert. Die lineare Approximation einer Funktion selbst ist aber anschließend eine einfache Folgerung, siehe auch Taylorreihe.

eindimensionaler Fall: \(y = f(x)\)

Beispiel: \(y = f(x) = x^2\), lineare Approximation bei \(x_0 = 1\), Inputänderung \(\Delta x = 1\)

Code

# Funktion f(x):
def my_f(x):
    return x**2

# erste Ableitung f'(x):
def my_f_p(x):
    return 2*x

# Vektor von x-Werten zum Plotten:
x = np.linspace(-2.1, 2.1) 

# Stelle der Approximation:
x0 = 1
y0 = my_f(x0)

# Änderungen:
delta_x = 1          # frei gewählte Änderung in der unabhängigen Größe x
dx      = delta_x    # Die lineare Approximation von delta_x ist gleich delta_x,
                     # da x eine unabhängige Größe ist.
#print("delta_x = ", delta_x)
#print("dx      = ", dx)

delta_y = my_f(x0 + dx) - my_f(x0)   # wahre Änderung, nicht linear approximiert
dy      = my_f_p(x0)*dx              # lineare Approximation von delta_y

#print("delta_y = ", delta_y)
#print("dy      = ", dy)

# Graph:
plt.figure()
plt.plot(x, my_f(x), color='black')
plt.plot(x0, y0, 'o', color='green')
plt.plot(x0 + dx, y0 + delta_y, 'o', color='red',label='Wahrer Wert')
plt.plot(x0 + dx, 3, 'o', color='blue',label='Approximation')
plt.arrow(x0,      y0, dx,      0, width=0.007, length_includes_head=True, color='blue')
plt.arrow(x0 + dx, y0, 0, delta_y, width=0.007, length_includes_head=True, color='red')
plt.arrow(x0 + dx, y0, 0,      dy, width=0.007, length_includes_head=True, color='blue')
plt.arrow(x0     , y0, dx,     dy, width=0.007, length_includes_head=True, color='blue')
plt.axis('equal')
plt.ylim(-.5, 4.5)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)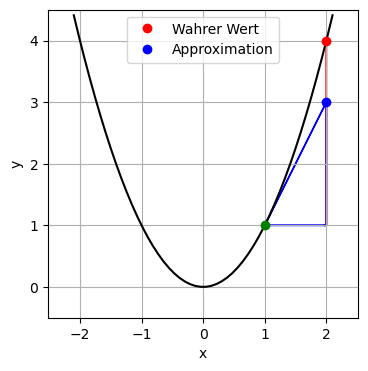

Nomenklatur:

• \(x_0\) ist die Stelle (Argument, Input), an der die Änderung der Funktion linear approximiert wird.
• \(\Delta x\) ist die frei gewählte Differenz (Änderung) der unabhängigen Inputgröße (Variablen) \(x\) bei \(x_0\).
• \(\text{d}x\) ist die lineare Approximation von \(\Delta x\). Da \(x\) keine Funktion einer anderen Größe ist, d. h. \(x\) ist eine unabhängige Variable, ist die Approximation fehlerfei und man erhält \(\text{d}x = \Delta x\). Wir schreiben vorwiegend \(\text{d}x\).
• \(\Delta y\) ist die wahre Differenz (Änderung) der Outputgröße \(y\) bei Änderung der Inputgröße um \(\Delta x\) bei \(x_0\).
• \(\text{d}y\) ist die lineare Approximation von \(\Delta y\).

Erste Ableitung:

Die erste Ableitung \(f'(x_0)\) der Funktion \(f\) bei \(x_0\) gibt die Änderungsrate von \(f\) bei \(x_0\) pro \(x\)-Einheit an und entspricht der Steigung der Tangente an den Graphen von \(f\) bei \(x_0\). Wird die Stelle \(x_0\) nicht spezifiziert, so erhält man eine Funktion von \(x\) und schreibt \(f'(x)\) oder kurz \(f'\). Oft wird auch \(y'(x_0)\), \(y'(x)\), \(y'\), \(\dot{y}(x_0)\), \(\dot{y}(x)\), oder \(\dot{y}\) verwendet.

mehrdimensionaler Fall: \(z = f(x, y)\)

Beispiel: \(z = f(x,y) = 0.05(x - 5)^2\sqrt{1 + y^2}\). Achtung: Wir verwenden im Folgenden zur grafischen Darstellung statt eines Graphen einen Konturplot!

Code

a = 0.05

def my_f(x, y):
    return a*(x - 5)**2*np.sqrt(1 + y**2)

def my_f_grad(x, y):
    return a*2*(x - 5)*np.sqrt(1 + y**2), a*(x - 5)**2*y/np.sqrt(1 + y**2)

x = np.linspace(-4, -1, 200)
y = np.linspace(-3,  0, 200)
X, Y = np.meshgrid(x, y)
Z = my_f(X, Y)

# Stelle:
x0 = -2
y0 = -1

# Konturplot:
plt.figure()
cs = plt.contour(X, Y, Z, np.arange(0, 20, 0.5), linewidths=2, cmap='coolwarm_r')
plt.clabel(cs, fontsize=10, fmt='%1.1f')
plt.plot(x0, y0,'o', color='black')
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
plt.grid(True)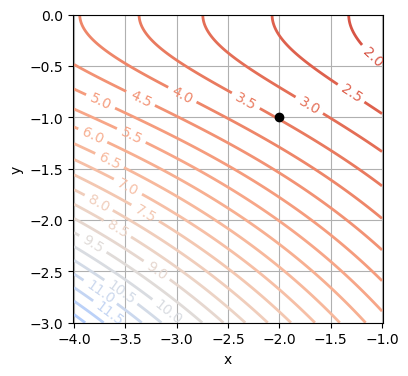

Code

# wahre Differenz:
delta_Z = Z - my_f(x0, y0)

# Gradient (Vektor der partiellen Ableitungen) an der Stelle:
gx, gy = my_f_grad(x0, y0)
print("Gradient:\n  x-Komponente = {:.2f}\n  y-Komponente = {:.2f}".format(gx, gy))

# totales Differential: linear approximierte Differenz
dX = X - x0
dY = Y - y0

dZ = gx*dX + gy*dY

# Konturplots:
plt.figure()
plt.plot(x0, y0,'ok')
plt.arrow(x0, y0, gx, gy, linewidth = 2)
cs = plt.contour(X, Y, delta_Z, np.arange(-5, 15, 0.5), linewidths=2, cmap='coolwarm_r')
plt.clabel(cs, fontsize=10, fmt='%1.1f')
cs = plt.contour(X, Y, dZ, np.arange(-5, 15, 0.5), linewidths=1, alpha=0.75, cmap='coolwarm_r')
plt.clabel(cs, fontsize=10, fmt='%1.1f')
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
plt.grid(True)

Gradient:
  x-Komponente = -0.99
  y-Komponente = -1.73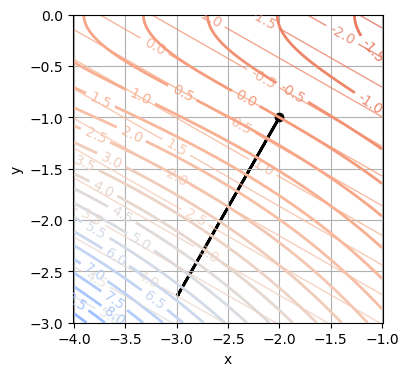

Nomenklatur:

• \((x_0, y_0)\) ist die Stelle (Argument, Input), an der die Änderung der Funktion linear approximiert wird.
• \(\Delta x\) ist die Differenz (Änderung) der Inputgröße \(x\) bei \((x_0, y_0)\), \(\Delta y\) ist die Differenz (Änderung) der Inputgröße \(y\) bei \((x_0, y_0)\).
• \(\text{d}x\) ist die lineare Approximation von \(\Delta x\), \(\text{d}y\) ist die lineare Approximation von \(\Delta y\). Es gilt analog zum eindimensionalen Fall \(\text{d}x = \Delta x\) und \(\text{d}y = \Delta y\). Wir schreiben vorwiegend \(\text{d}x\) und \(\text{d}y\).
• \(\Delta z\) ist die wahre Differenz (Änderung) der Outputgröße \(z\) bei Änderung der Inputgröße um \(\Delta x\) und \(\Delta y\) bei \((x_0, y_0)\).
• \(\text{d}z\) ist die lineare Approximation von \(\Delta z\).

\(\Delta z\) hängt im allgemeinen nicht-linear von \(\text{d}x\) und \(\text{d}x\) ab. Die lineare Approximation \(\text{d}z\) dieser Abhängigkeit ist für zweidimensionale Funktionen von der Form \(\text{d}z = k_x\,\text{d}x + k_y\,\text{d}y\) für bestimmte Zahlen \(k_x\) und \(k_y\). Diese Zahlen sind die partiellen Ableitung \(\frac{\partial f}{\partial x}(x_0, y_0)\) und \(\frac{\partial f}{\partial y}(x_0, y_0)\) der Funktion \(f\) bei \((x_0, y_0)\) nach \(x\) und nach \(y\).

Bemerkungen:

• Für nicht-lineare Funktionen gilt im Allgemeinen \(\Delta z \neq \text{d}z\).
• Für lineare Funktionen gilt immer \(\Delta z = \text{d}z\).
• Je kleiner \(\text{d}x\) und \(\text{d}y\) umso besser approximiert \(\text{d}z\) den wahren Wert \(\Delta z\).

partielle Ableitungen:

• Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(x\) wird als \(\frac{\partial f}{\partial x}(x_0, y_0)\) geschrieben. Sie gibt die Änderungsrate von \(f\) bei \((x_0, y_0)\) pro \(x\)-Einheit an und entspricht der Steigung der Tangente in \(x\)-Richtung an den Graphen von \(f\) bei \((x_0, y_0)\). Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(x\) wird durch Konstanthalten von \(y\) und Ableiten nach \(x\) berechnet.

• Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(y\) wird als \(\frac{\partial f}{\partial y}(x_0, y_0)\) geschrieben. Sie gibt die Änderungsrate von \(f\) bei \((x_0, y_0)\) pro \(y\)-Einheit an und entspricht der Steigung der Tangente in \(y\)-Richtung an den Graphen von \(f\) bei \((x_0, y_0)\). Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(y\) wird durch Konstanthalten von \(x\) und Ableiten nach \(y\) berechnet.

Wird die Stelle \((x_0, y_0)\) nicht spezifiziert, so erhält man pro partieller Ableitung eine Funktion von \(x\) und \(y\) und schreibt z. B. \(\frac{\partial f}{\partial x}(x, y)\) oder kurz \(\frac{\partial f}{\partial x}\). Oft wird auch \(\frac{\partial z}{\partial x}(x_0, y_0)\), \(\frac{\partial z}{\partial x}(x, y)\) und \(\frac{\partial z}{\partial x}\) verwendet.

Beispiel:

Für \(z = f(x,y) = 3x^2y - y^2\) ist \(\frac{\partial f}{\partial x} = 6xy\) und \(\frac{\partial f}{\partial y} = 3x^2 - 2y\). An der Stelle \((x_0, y_0) = (1,2)\) ergeben sich die Werte \(\frac{\partial f}{\partial x}(1,2) = 12\) und \(\frac{\partial f}{\partial y}(1,2) = -1.\)

Gradient:

An die Stelle der ersten Ableitung \(f'\) im eindimensionalen Fall tritt im zweidimensionalen Fall der Gradient. Der Gradient \(\text{grad}(f)\) ist der Vektor der partiellen Ableitungen. Wir schreiben ihn immer als Spaltenvektor:

\[\text{grad}(f) = \begin{pmatrix}\frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y}\end{pmatrix}.\]

Der Gradient an der Stelle \((x_0, y_0)\) ist der Koeffizientenvektor der linearen Approximation \(\text{d}z\) von \(\Delta z\). Aus der linearen Algebra wissen wir, dass die Konturlinien der linearen Approzimation \(\text{d}z\) parallele, äquidistante Geraden sind und der Koeffizientenvektor, also der Gradient, orthogonal auf die Konturlinien ist und in die Richtung der stärksten Zunahme von \(\text{d}z\) zeigt.

Nabla Operator:

• Eine andere und ebenfalls übliche Schreibweise für den Gradienten \(\text{grad}(f)\) einer Funktion \(f\) ist \(\nabla f\), wobei \(\nabla\) der sogenannte Nabla-Operator ist:

  \[\nabla = \begin{pmatrix}\frac{\partial}{\partial x} \\ \frac{\partial}{\partial y}\end{pmatrix}\]

• Statt z. B. \(\frac{\partial f}{\partial x}\) wird oft die Kurzschreibweise \(f_x\) oder \(f_{|x}\) verwendet.

• Statt dem Funktionsnamen wird im ein- und mehrdimensionalen Fall oft der Name der Outputgröße verwendet und umgekehrt, z. B., \(\text{grad}(z)\) statt \(\text{grad}(f)\) oder \(\text{d}f\) statt \(\text{d}z\).

Vollständiges (totales) Differential:

Die lineare Approximation \(\text{d}z\) wird als das totale Differential, oder kurz das Differential von \(z\) bezeichnet. Es kann als inneres Produkt des Gradienten mit dem Vektor der Inputgößenänderungen geschrieben werden:

\[\text{d}z = \frac{\partial f}{\partial x}\,\text{d}x + \frac{\partial f}{\partial y}\,\text{d}y = \begin{pmatrix}\frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y}\end{pmatrix}^T \begin{pmatrix}\text{d}x \\ \text{d}y \end{pmatrix}\]

Beispiel:

Für \(z = f(x,y) = 3x^2y - y^2\) und \((x_0, y_0) = (1,2)\) ergeben sich:

• \(\text{grad}(f) = \nabla f = \begin{pmatrix} 6xy \\ 3x^2 - 2y \end{pmatrix}\)

• \(\text{grad}(f)(1,2) = \nabla f(1,2) = \begin{pmatrix} 12 \\ -1 \end{pmatrix}\)

• \(\text{d}z = 6xy\,\text{d}x + (3x^2 - 2y)\,\text{d}y\)

• bei \((1,2)\) ist \(\text{d}z = 12\,\text{d}x - \text{d}y\)

• mit zusätzlich \(\text{d}x = 0.1\) und \(\text{d}y = 0.2\):

  • \(\Delta z = f(1.1, 2.2) - f(1,2) = 1,146\)
  • \(\text{d}z = 12\cdot 0.1 - 0.2 = 1\)

Rechnen mit Differentialen

Beispiele:

Beispiel 1: Rotation eines Punktes bei konstantem Radius R: Zwei skalare Funktionen, die von der selben unabhängigen Variablen abhängen: \(x(t) = R \cdot \cos(\omega t)\) und \(y(t) = R \cdot \sin(\omega t)\):

\[\begin{align} \text{d}x &= -R\omega\sin(\omega t)\,\text{d}t \\ \text{d}y &= R\omega\cos(\omega t)\,\text{d}t \end{align}\]

in Vektorform:

\[\begin{pmatrix} \text{d}x \\ \text{d}y \end{pmatrix} = \begin{pmatrix} -R\omega\sin(\omega t) \\ R\omega\cos(\omega t) \end{pmatrix} \text{d}t\]

und nach Division durch \(\text{d}t\):

\[\begin{pmatrix} \frac{\text{d}x}{\text{d}t} \\ \frac{\text{d}y}{\text{d}t} \end{pmatrix} = \begin{pmatrix} -R\omega\sin(\omega t) \\ R\omega\cos(\omega t) \end{pmatrix}\]

Falls \(x\) und \(y\) Ortskoordinaten sind und \(t\) die Bedeutung Zeit hat, dann ist dies der Geschwindigkeitsvektor. \(R\omega=v_\mathrm{t}\) entspricht dem Betrag des tangential an die Kreisbahn anliegenden Geschwindigkeitsvektors.

Beispiel 2: Polarkoordinaten (zwei unabhängige Variablen \(r,\varphi\)): \(x(r,\varphi) = r\cos(\varphi)\) und \(y(r, \varphi) = r\sin(\varphi)\):

\[\begin{align} \text{d}x &= \cos(\varphi)\,\text{d}r - r\sin(\varphi)\,\text{d}\varphi \\ \text{d}y &= \sin(\varphi)\,\text{d}r + r\cos(\varphi)\,\text{d}\varphi \end{align}\]

in Matrixform:

\[\begin{pmatrix} \text{d}x \\ \text{d}y \end{pmatrix} = \begin{pmatrix} \cos(\varphi) & - r\sin(\varphi) \\ \sin(\varphi) & r\cos(\varphi) \end{pmatrix} \begin{pmatrix} \text{d}r \\ \text{d}\varphi \end{pmatrix}\]

Die \(2\times 2\) Matrix \(\begin{pmatrix} \cos(\varphi) & - r\sin(\varphi) \\ \sin(\varphi) & r\cos(\varphi) \end{pmatrix}\) ist die sogenannte Jacobimatrix der Funktion \(f:\mathbb{R}^2 \rightarrow \mathbb{R}^2: \begin{pmatrix} r \\ \varphi \end{pmatrix} \mapsto \begin{pmatrix} r\cos(\varphi) \\ r\sin(\varphi) \end{pmatrix}\). Die Jacobimatrix enthält alle partiellen Ableitungen:

\[\begin{pmatrix} \cos(\varphi) & - r\sin(\varphi) \\ \sin(\varphi) & r\cos(\varphi) \end{pmatrix} = \begin{pmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \varphi} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \varphi} \end{pmatrix}\]

Mehrdimensionale Funktionen

Themenüberblick:

• Skalarfelder: Graph, Konturlinien, lineares Skalarfeld
• Kurven: Geschwindigkeit, Beschleunigung, Tangente
• Oberflächen: Parametrisierung, Tangentialebene, Normalvektor, Kugel- und Zylinderkoordinaten
• Vektorfelder: Divergenz und Rotation von Vektorfeldern

Skalarfelder

Ein Skalarfeld auf \(\mathbb{R}^n\) ist eine Funktion \(f:\mathbb{R}^n \rightarrow \mathbb{R}\). Jedem Element, typischerweise als Punkt oder Ort interpretiert, in \(\mathbb{R}^n\) wird also eine Zahl zugeordnet. Anders ausgedrückt wird jeder Punkt \(x\in\mathbb{R}^n\) mit der Zahl \(f(x)\) eindeutig bewertet.

Beispiele:

• Abstand eines Punktes der Ebene vom Ursprung: \(r:\mathbb{R}^2 \rightarrow \mathbb{R}: r(x,y) = \sqrt{x^2 + y^2}.\)
• Druck oder Temperatur in einem Raum als Funktion der kartesischen Raumkoordinaten \(p:\mathbb{R}^3 \rightarrow \mathbb{R}:p(x,y,z)\), \(T:\mathbb{R}^3 \rightarrow \mathbb{R}:T(x,y,z)\)
• Wir lösen die Zustandsgleichung \(pV=nRT\) des idealen Gases nach \(T\) auf und behandeln \(p\) und \(V\) als unabhängige Größen und \(n\) als konstant: \(T:\mathbb{R}^2 \rightarrow \mathbb{R}: T(p,V) = \frac{pV}{nR}.\)
• Allgemeines lineares Skalarfeld: \(f:\mathbb{R}^n \rightarrow \mathbb{R}: f(x)=c^T x\) für einen fixen Koeffizientenvektor \(c\in\mathbb{R}^n\).

Grafische Darstellungsmöglichkeiten:

• als Graph
• mit Konturlinien bzw. Kontur(hyper)flächen: Bei linearen Skalarfeldern sind das parallele Geraden bzw. (Hyper)ebenen.

Code

x = np.linspace(-3, 3, 200)
y = np.linspace(-3, 3, 200)
X, Y = np.meshgrid(x, y)
Z = X*Y*np.exp(-0.5*(X**2 + Y**2))

fig = plt.figure(figsize=(8,4))
ax  = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_surface(X, Y, Z, rstride=4, cstride=4, linewidth=0, cmap=plt.cm.coolwarm)
ax.view_init(azim = -60, elev = 30)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax2 = fig.add_subplot(1, 2, 1)
cs = ax2.contour(X, Y, Z, 15, cmap= 'coolwarm');
ax2.clabel(cs, inline=1)
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.grid(True)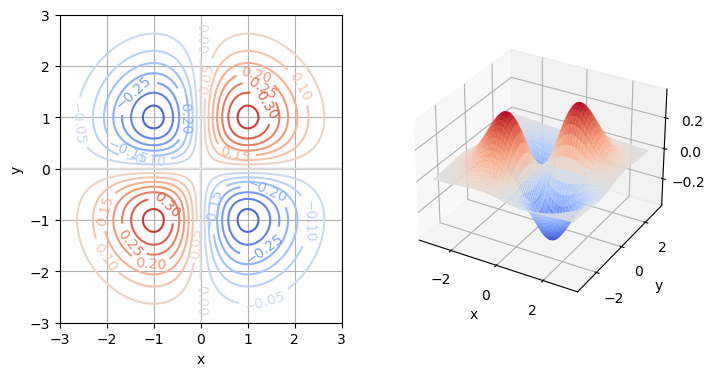

Kurven

Eine Kurve in \(\mathbb{R}^n\) ist eine Funktion \(f:\mathbb{R} \rightarrow \mathbb{R}^n\). Jedem Element, typischerweise als Zeitpunkt interpretiert, in \(\mathbb{R}\) wird also eine Element in \(\mathbb{R}^n\), typischerweise als Ort interpretiert, zugeordnet.

Beispiele:

• Bewegung eines Massenpunktes: Kurve im Raum, auf einer Oberfläche etc.
• thermodynamischer Prozess: Kurve im Zustandsraum
• Gerade in der Ebene: Die aus der Schule bekannte Geradengleichung in Parameterform \(\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 5 \\ 0 \end{pmatrix} + t \begin{pmatrix} 4 \\ -3 \end{pmatrix}\) entspricht der Funktion \(f:\mathbb{R} \rightarrow \mathbb{R}^2: f(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix} = \begin{pmatrix} 5 + 4t \\ -3t \end{pmatrix}\)
• Die nach \(x\) parametrisierte Kurve entlang des Graphen der eindimensionalen Funktion \(y(x) = x^2 - \sin(x)\) ist die Funktion \(f:\mathbb{R} \rightarrow \mathbb{R}^2: f(x) = \begin{pmatrix} x \\ y(x) \end{pmatrix} = \begin{pmatrix} x \\ x^2 - \sin(x) \end{pmatrix}\)
• Die nach \(y\) parametrisierte Kurve entlang des Graphen der eindimensionalen Funktion \(x(y) = \cos(y)\) ist die Funktion \(f:\mathbb{R} \rightarrow \mathbb{R}^2: f(y) = \begin{pmatrix} x(y) \\ y \end{pmatrix} = \begin{pmatrix} \cos(y) \\ y \end{pmatrix}\)
• Die Kreisbahn mit Radius \(r\) und Kreisfrequenz \(\omega\) ist die Funktion \(f:\mathbb{R} \rightarrow \mathbb{R}^2: f(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix} = \begin{pmatrix} r\cos(\omega t) \\ r\sin(\omega t) \end{pmatrix}\)
• Die Funktion \(f:\mathbb{R} \rightarrow \mathbb{R}^3: f(t) = \begin{pmatrix} x(t) \\ y(t) \\ z(t) \end{pmatrix} = \begin{pmatrix} r\cos(\omega t) \\ r\sin(\omega t) \\ t \end{pmatrix}\) ist eine Schraubenlinie im Raum.

Code

#Wir plotten die Schraubenlinie:

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
t = np.linspace(-4*np.pi, 4*np.pi, 200)
x = np.cos(t)
y = np.sin(t)
z = t
ax.plot(x, y, z,color='darkred',ls='dashed')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');

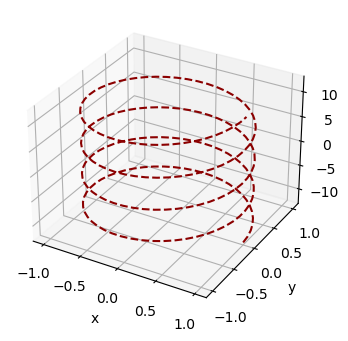
Wird die Inputvariable als Zeitpunkt interpretiert und die Outputvariablen als Ort, so ist die erste Ableitung der Kurve die Geschwindigkeit und die zweite Ableitung die Beschleunigung der von der Kurve beschriebenen Bewegung.

Beispiel: Kreisbahn mit Radius \(r\) und Kreisfrequenz \(\omega\): - Ort: \(\begin{pmatrix} x(t) \\ y(t) \end{pmatrix} = \begin{pmatrix} r\cos(\omega t) \\ r\sin(\omega t) \end{pmatrix}\) - Geschwindigkeit = Tangentialvektor: \(\begin{pmatrix} \dot{x}(t) \\ \dot{y}(t) \end{pmatrix} = \begin{pmatrix} -r\omega\sin(\omega t) \\ r\omega\cos(\omega t) \end{pmatrix}\) - Beschleunigung: \(\begin{pmatrix} \ddot{x}(t) \\ \ddot{y}(t) \end{pmatrix} = \begin{pmatrix} -r\omega^2\cos(\omega t) \\ -r\omega^2\sin(\omega t) \end{pmatrix} = -\omega^2\begin{pmatrix} x(t) \\ y(t) \end{pmatrix}\) - Tangente bei \(t\) in Parameterform mit Parameter \(s\): \(\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} r\cos(\omega t) \\ r\sin(\omega t) \end{pmatrix} + s \begin{pmatrix} -r\omega\sin(\omega t) \\ r\omega\cos(\omega t) \end{pmatrix}\)

Code

#Darstellung der Kreisbewegung eines Punktes bei konstantem Radius

omega = 0.75
r = 1.3
t = np.linspace(0, 2*np.pi/omega, num=30)
x = r*np.cos(omega*t)
y = r*np.sin(omega*t)
xp = -r*omega*np.sin(omega*t)
yp =  r*omega*np.cos(omega*t)
xpp = -r*omega**2*np.cos(omega*t)
ypp = -r*omega**2*np.sin(omega*t)

plt.figure()
plt.plot(x, y, color='black', label='Ort')
plt.quiver(x, y, xp , yp , scale_units='xy', scale= 1, color='blue', label='Geschwindigkeit')
plt.quiver(x, y, xpp, ypp, scale_units='xy', scale= 1, color='red', label='Beschleunigung')
plt.legend(loc=1, fontsize=9)
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)
plt.grid(True)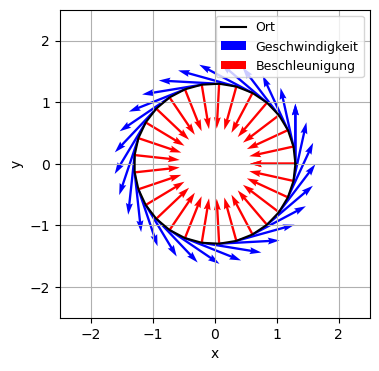

Oberflächen

Eine (parametrisierte) Oberfläche im \(\mathbb{R}^3\) ist eine Funktion \(f:\mathbb{R}^2 \rightarrow \mathbb{R}^3\). Jedem Parameterpaar \((u,v)\) in \(\mathbb{R}^2\) wird ein Ort \(f(u,v)\) im \(\mathbb{R}^3\) zugeordnet.

Beispiele:

• Ebene im Raum: Die aus der Schule bekannte Ebenengleichung in Parameterform \(X = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 8 \\ 4 \end{pmatrix} + s \begin{pmatrix} -1 \\ 4 \\ 5 \end{pmatrix} + t \begin{pmatrix} 2 \\ -1 \\ 7 \end{pmatrix}\) entspricht der Funktion \(f:\mathbb{R}^2 \rightarrow \mathbb{R}^3: f(s, t) = \begin{pmatrix} x(s, t) \\ y(s, t) \\ z(s, t) \end{pmatrix} = \begin{pmatrix} 3 -s + 2t \\ 8 + 4s -t \\ 4 + 5s + 7t \end{pmatrix}\) mit den Parametern \(s\) und \(t\).
• Kugeloberfläche mit konstantem Radius \(R\): Als Parameter werden meist die zwei Winkel \(\vartheta\) und \(\varphi\) der Kugelkoordinaten verwendet: \(f:\mathbb{R}^2 \rightarrow \mathbb{R}^3: f(\vartheta, \varphi) = \begin{pmatrix} x(\vartheta, \varphi) \\ y(\vartheta, \varphi) \\ z(\vartheta, \varphi) \end{pmatrix} = \begin{pmatrix} R\sin(\vartheta)\cos(\varphi) \\ R\sin(\vartheta)\sin(\varphi) \\ R\cos(\vartheta) \end{pmatrix}.\)
• Zylindermantel mit konstantem Radius \(R\): Als Parameter werden meist der Winkel \(\varphi\) und die Höhe \(z\) der Zylinderkoordinaten verwendet: \(f:\mathbb{R}^2 \rightarrow \mathbb{R}^3: f(\varphi, z) = \begin{pmatrix} x(\varphi, z) \\ y(\varphi, z) \\ z(\varphi, z) \end{pmatrix} = \begin{pmatrix} R\cos(\varphi) \\ R\sin(\varphi) \\ z \end{pmatrix}.\)

Code

# Zylindermantel:
r = 3
phi = np.linspace(-np.pi, np.pi, 200)
z   = np.linspace(  0,  2, 200)
PHI, Z = np.meshgrid(phi, z)
X = r*np.cos(PHI)
Y = r*np.sin(PHI)

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_surface(X, Y, Z, alpha=0.2)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');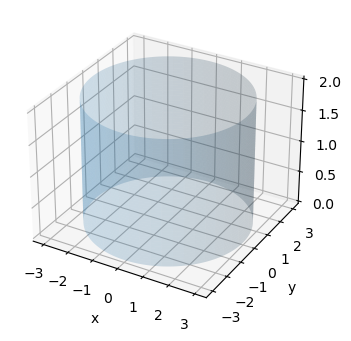

Vektorfelder

Ein Vektorfeld auf \(\mathbb{R}^n\) ist eine Funktion \(f:\mathbb{R}^n \rightarrow \mathbb{R^n}\). Jedem Element, typischerweise als Punkt oder Ort interpretiert, in \(\mathbb{R}^n\) wird also ein Vektor zugeordnet.

Beispiele:

• Kraftfelder (auf einen Körper wirkende Gravitationskraft der Erde) \(f:\mathbb{R}^3 \rightarrow \mathbb{R^3}:\begin{pmatrix}x\\y\\z\end{pmatrix}= \begin{pmatrix}0\\0\\-m\cdot g\end{pmatrix}\) mit der Masse \(m\) und der Erdbeschleunigung \(g=9.81\) m/s²
• Geschwindigkeitsfelder
• Elektromagnetisches Feld

Grafische Darstellungsmöglichkeiten:

• in Python: Quiver-Plot

Divergenz und Rotation von Vektorfeldern:

Die Divergenz eines Vektorfelds berechnet, ob sich im Vektorfeld Quellen oder Senken befinden. Die Divergenz berechnet sich als das innere Produkt zwischen dem Nabla-Operator \(\nabla\) und dem Vektorfeld \(f\) zu:

\(\nabla \cdot f=\begin{pmatrix} \partial/\partial x \\ \partial/\partial y \\ \partial/\partial z\end{pmatrix} \cdot \begin{pmatrix} f_x \\ f_y \\ f_z\end{pmatrix} = \partial f_x/\partial x + \partial f_y/\partial y + \partial f_z/\partial z\)

Als Ergebnis erhalten wir ein Skalarfeld.

Beispiel:

\[f=\begin{pmatrix} x \\ y \end{pmatrix}\]

\[\text{div}(f)=\nabla \cdot f=1+1=2\]

Ergibt die Divergenz eines Vektorfelds nicht 0, so spricht man von einem Quellfeld.

Die Rotation eines Vektorfelds berechnet, ob sich im Vektorfeld Wirbel befinden. Wir sprechen dann von einem Wirbelfeld. Die Divergenz berechnet sich als das Kreuzprodukt zwischen dem Nabla-Operator \(\nabla\) und dem Vektorfeld \(f\) zu:

\(\nabla \times f=\begin{pmatrix} \partial/\partial x \\ \partial/\partial y \end{pmatrix} \times \begin{pmatrix} f_x \\ f_y \end{pmatrix} = \begin{pmatrix} \partial f_y/\partial x - \partial f_x/\partial y \end{pmatrix}\)

Die Rotation eines 2-dimensionalen Vektorfelds ergibt ein Skalarfeld. Die Rotation eines 3-dimensionalen (oder höherdimensionalen) Vektorfelds ergibt wieder ein Vektorfeld.

Beispiel:

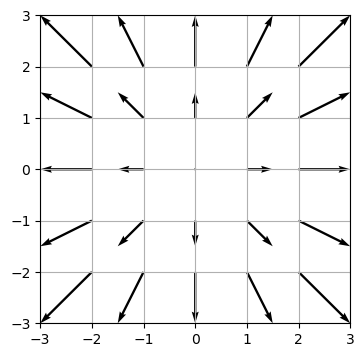
\[f=\begin{pmatrix} y \\ -x \end{pmatrix}\]

\[\text{rot}(f)=\nabla \times f=\begin{pmatrix} \partial (-x)/\partial x - \partial (y)/\partial y \end{pmatrix}=-1-1=-2\]

Das betrachtete Vektorfeld ist somit ein Wirbelfeld, was wir auch in der grafischen Darstellung erkennen können. Nachfolgend sind die beiden Vektorfelder dargestellt:

Code

# Hier ist ein Quellfeld dargestellt:

x=np.arange(-3,3.1,1)
y=np.arange(-3,3.1,1)

X,Y=np.meshgrid(x,y)

U,V=X,Y

fig = plt.figure()
ax = fig.add_subplot()
ax.quiver(X, Y, U, V,angles='xy', scale_units='xy', scale=2)
ax.set_xlim(-3,3)
ax.set_ylim(-3,3)
ax.grid(True)

Code

#Hier ist ein Wirbelfeld dargestellt:

x=np.arange(-3,3.1,1)
y=np.arange(-3,3.1,1)

X,Y = np.meshgrid(x,y)
U,V = [Y,-X]

fig,ax = plt.subplots()
q=ax.quiver(X, Y, U,V,angles='xy', scale_units='xy', scale=2)
ax.set_xlim(-3,3)
ax.set_ylim(-3,3)
ax.grid(True)

Arbeitsintegrale

Themenüberblick:

• Mechanik und Elektrodynamik: Kraftvektorfeld, Weg, Arbeit
• Thermodynamik: Differential, Prozess, Arbeit, Wärme
• Berechnungsvarianten
• Wegunabhängigkeit: Kriterium
• Potentialfunktionen

Mechanik und Elektrodynamik

Um in der Mechanik und in der Elektrodynamik die Arbeit \(W\) zu bestimmen, die von einer ortsabhängigen Kraft an einem Teilchen entlang eines beliebigen Weges geleistet wird, wird ein sogenanntes Arbeitsintegral berechnet. Dabei wird die ortsabhängige Kraft als Vektorfeld \(F:\mathbb{R}^n \rightarrow \mathbb{R}^n\) modelliert und der Weg als Kurve \(s:\mathbb{R} \rightarrow \mathbb{R}^n\). Die Dimension \(n\) ist zwei für eine Berechnung in der Ebene und drei für eine Berechnung im Raum.

Um den Arbeitsanteil entlang einer kurzen Wegdifferenz \(\text{d}s\) (Wegstück, kurze Strecke) zu erhalten, wird die vektorielle Kraft \(F\) am entsprechenden Ort mit der kurzen vektoriellen Wegdifferenz \(\text{d}s\) im Sinn des inneren Produktes multipliziert. Dadurch wird nur der Anteil der Kraft in Richtung der Wegdifferenz berücksichtigt. Die gesamte Arbeit ist die Summe aller Arbeitsanteile im Grenzwert, dass die einzelnen Wegdifferenzen beliebig klein angenommen werden. Somit erhalten wir das Arbeitsintegral

\[W = \int F^T \text{d}s.\]

Oft wird das innere Produkt statt in Matrixschreibweise mit dem transponierten Kraftvektor mit einem Punkt (englisch “dot product”) zwischen dem Kraftvektor und dem Wegstück geschrieben:

\[W = \int F \cdot \text{d}s.\]

Beispiel:

Kraft \(F:\mathbb{R}^2 \rightarrow \mathbb{R}^2: F(x, y) =\begin{pmatrix} F_x (x,y) \\ F_y (x,y) \end{pmatrix} = \begin{pmatrix} yx \\ -x \end{pmatrix}\), Weg \(s:\mathbb{R} \rightarrow \mathbb{R}^2: s(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix} = \begin{pmatrix} 4t^2 \\ 3t \end{pmatrix}\).

Zum Zeitpunkt \(t\) ist das Teilchen am Ort \(s(t)\) und die Kraft hat den Wert \(F(s(t))= \begin{pmatrix} 3t4t^2 \\ -4t^2 \end{pmatrix} = \begin{pmatrix} 12t^3 \\ -4t^2 \end{pmatrix}.\) Die Wegdifferenz ist zum selben Zeitpunkt durch \(\text{d}s = \begin{pmatrix} 8t\,\text{d}t \\ 3\,\text{d}t \end{pmatrix} = \begin{pmatrix} 8t \\ 3 \end{pmatrix}\text{d}t\) gegeben. Wir berechnen die von \(F\) entlang \(s\) verrichtete Arbeit zwischen den Zeitpunkten \(t_1=0\) und \(t_2=1\):

\[\begin{align} W &= \int F \cdot \text{d}s \\ &= \int_0^1 \begin{pmatrix} 12t^3 \\ -4t^2 \end{pmatrix} \cdot \begin{pmatrix} 8t \\ 3 \end{pmatrix} \text{d}t \\ &= \int_0^1 (12t^3 8t - 4t^2 3) \,\text{d}t \\ &= \int_0^1 (96t^4 - 12t^2) \,\text{d}t \\ &= \frac{96}{5} - \frac{12}{3} = 15.2 \end{align}\]

Code

#Wir stellen die Wegstrecke im Kraftfeld als rote Linie dar

x = np.arange(-1, 4.5, 0.5)
y = np.arange(-1, 4.5, 0.5)
X, Y = np.meshgrid(x, y)
Fx = X*Y
Fy = -X

t = np.linspace(0, 1)
x = 4*t**2
y = 3*t

plt.figure()
Q = plt.quiver(X, Y, Fx, Fy, units='xy', scale=8)
plt.plot(x, y, 'r')
plt.xlabel('x')
plt.ylabel('y')
plt.ylim(-.2, 3.8)
plt.grid(True)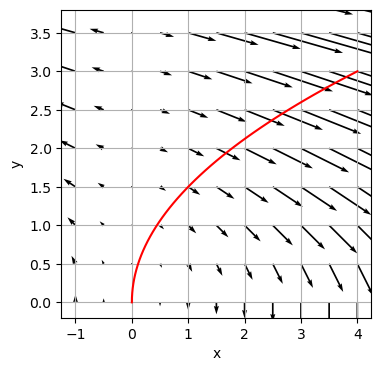

Wir schreiben das Arbeitsintegral detaillierter, indem wir das innere Produkt ausschreiben:

\[W = \int F \cdot \text{d}s = \int F_x (x,y)\,\text{d}x + F_y (x,y)\,\text{d}y.\]

Im obigen Beispiel bedeutet das \(W = \int F \cdot \text{d}s = \int yx \text{d}x - x \text{d}y.\)

Es gilt aber auch \(W=\int dW\). Somit entspricht das Arbeitsdifferential einem vollständigen Differential, in welchem die partiellen Ableitungen die Komponenten des Kraftfelds sind:

\(dW=F_x(x,y)\cdot \text{d}x+F_y(x,y)\cdot \text{d}y\)

Thermodynamik

In der Thermodynamik wird dieselbe Mathematik mit anderen Begriffen verwendet: Statt Kraftfeldern verwendet man Differentiale, statt von Wegen spricht man von Prozessen.

Beispiel:

Ein Mol eines einatomigen idealen Gases erfüllt die Zustandsgleichung \(pV=RT\). Zur Beschreibung des Zustands verwenden wir die beiden Zustandsgrößen \(p\) (Druck) und \(V\) (Volumen) als Koordinaten des Zustandsraums (= Menge aller Gleichgewichtszustände des Gases). Damit lassen sich die Zustandsgrößen \(T\) (Temperatur), \(U\) (innere Energie) und \(S\) (Entropie) als folgende Funktionen auf dem Zustandsraum schreiben:

• Temperatur \(T(p,V) = \frac{pV}{R}\)
• innere Energie \(U(p,V) = \frac{3}{2}pV = \frac{3}{2}RT(p,V)\)
• Entropie \(S(p,V) = \frac{3}{2}R\ln(pV^{5/3})\)

Die Wärme \(Q\), die vom Gas bei einem Prozess aufgenommen wird, kann über das Arbeitsintegral

\[Q = \int T \,\text{d}S\]

berechnet werden. Der Prozess wird dabei durch eine bestimmte Kurve im Zustandsraum beschrieben.

Wir berechnen nun den Integranden \(T\,\text{d}S\) in den \((p,V)\)-Koordinaten:

\[\begin{align} T\,\text{d}S =& \frac{pV}{R} \left[ \frac{\partial S}{\partial p}\,\text{d}p + \frac{\partial S}{\partial V}\,\text{d}V \right] \\ =& \frac{pV}{R} \left[ \frac{3}{2}R\frac{1}{p}\,\text{d}p + \frac{3}{2}R \frac{5}{3}\frac{1}{V}\,\text{d}V \right] \\ =& \frac{3}{2}V\,\text{d}p + \frac{5}{2}p\,\text{d}V \end{align}\]

Der Integrand \(T\,\text{d}S = \frac{3}{2}V\,\text{d}p + \frac{5}{2}p\,\text{d}V\) ist die lineare Approximation jener Wärmemenge, die vom Gas aufgenommen wird, wenn es seinen Zustand von \((p,V)\) zu \((p + \text{d}p, V + \text{d}V)\) ändert. Je kleiner \(\text{d}p\) und \(\text{d}V\) umso genauer ist die Approximation. Dies ist in völliger Analogie zum Arbeitsanteil \(F_x (x,y)\,\text{d}x + F_y (x,y)\,\text{d}y\), den die Kraft entlang des Wegstückes von \((x,y)\) nach \((x + \text{d}x, y + \text{d}y)\) verrichtet.

Ein Ausdruck von der Form \(F_p (p,V)\,\text{d}p + F_V (p,V)\,\text{d}V\) bzw. \(F_x (x,y)\,\text{d}x + F_y (x,y)\,\text{d}y\) mit Funktionen \(F_p (p,V), F_V (p,V), F_x (x,y), F_y (x,y)\) wird allgemein Differential(form) in \((p,V)\) bzw. in \((x,y)\) genannt. Einem Differential kann man eindeutig ein Vektorfeld zuordnen und umgekehrt kann man jedem Vektorfeld ein Differential zuordnen:

• Dem Differential \(F_p (p,V)\,\text{d}p + F_V (p,V)\,\text{d}V\) in der \((p,V)\)-Ebene entspricht das Vektorfeld \(\begin{pmatrix} F_p (p,V) \\ F_V (p,V) \end{pmatrix}\).
• Dem Vektorfeld \(\begin{pmatrix} F_x (x,y) \\ F_y (x,y) \end{pmatrix}\) in der \((x,y)\)-Ebene entspricht das Differential \(F_x (x,y)\,\text{d}x + F_y (x,y)\,\text{d}y\).

Wir zeichnen nun das Vektorfeld des Wärmedifferentials \(T\,\text{d}S\) in der \((p,V)\)-Ebene (\((p,V)\)-Diagramm). Dabei wird typischer Weise \(p\) nach oben und \(V\) nach rechts gezeichnet. Zudem zeichnen wir den Prozess \(s(t) = \begin{pmatrix} p(t) \\ V(t) \end{pmatrix} = \begin{pmatrix} 2t \\ t^2 \end{pmatrix}\) für \(t_1=0.5\) bis \(t_2=1.5\) im \((p,V)\)-Diagramm ein.

Code

p = np.arange(0 ,4, 0.5)
V = np.arange(0, 4, 0.5)
V_, p_ = np.meshgrid(V, p)
Fp = 3/2*V_
FV = 5/2*p_

t = np.linspace(0.5, 1.5)
p = 2*t
V = t**2 

plt.figure()
Q = plt.quiver(V_,p_, FV, Fp, units='xy', scale=15)
plt.plot(V, p, 'r')
plt.xlabel('V')
plt.ylabel('p')
plt.ylim(-.2, 3.8)
plt.grid(True)

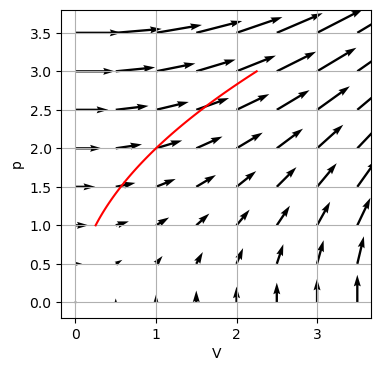
Die Wärme \(Q\) entlang des Prozesses wird über das “Arbeits”-integral \(Q = \int T \,\text{d}S = \int \frac{3}{2}V\,\text{d}p + \frac{5}{2}p\,\text{d}V\) wie folgt berechnet:

\[\begin{align} Q &= \int \frac{3}{2}V\,\text{d}p + \frac{5}{2}p\,\text{d}V \\ &= \int_{0.5}^{1.5} \frac{3}{2}t^2 2\,\text{d}t + \frac{5}{2}2t 2t\,\text{d}t \\ &= \int_{0.5}^{1.5} 13 t^2\,\text{d}t \\ &= \frac{13}{6}(1.5^3 - 0.5^3) = 7.04 \end{align}\]

Die Arbeit \(W\), die vom Gas bei einem Prozess geleistet wird, kann über das Arbeitsintegral

\[W = \int p \,\text{d}V\]

berechnet werden.

Wir zeichnen nun das Vektorfeld des Arbeitsdifferentials \(p\,\text{d}V\) in der \((p,V)\)-Ebene. Zudem zeichnen wir wieder den Prozesse \(s(t) = \begin{pmatrix} p(t) \\ V(t) \end{pmatrix} = \begin{pmatrix} 2t \\ t^2 \end{pmatrix}\) für \(t_1=0.5\) bis \(t_2=1.5\) ein.

Code

p = np.arange(0 ,4, 0.5)
V = np.arange(0, 4, 0.5)
V_, p_ = np.meshgrid(V, p)
FV = p_
Fp = 0*np.ones(V_.shape)

t = np.linspace(0.5, 1.5)
p = 2*t
V = t**2 

plt.figure()
Q = plt.quiver(V_,p_, FV, Fp, units='xy', scale=7)
plt.plot(V, p, 'r')
plt.xlabel('V')
plt.ylabel('p')
plt.ylim(-.2, 3.8)
plt.grid(True)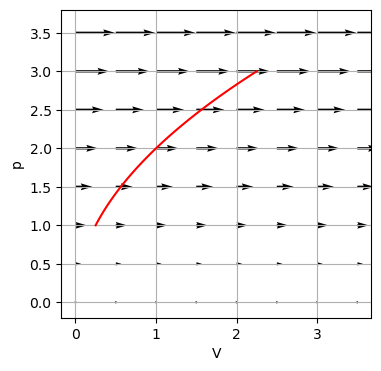

Wir sehen anhand des eingezeichneten Vektorfelds, dass die von einem System geleistete Arbeit mit zunehmendem Druck ebenfalls größer wird. Die Arbeit \(W\) entlang des Prozesses berechnet sich wie folgt:

\[\begin{align} W =& \int p\,\text{d}V \\ =& \int_{0.5}^{1.5} 2t 2t\,\text{d}t \\ =& \int_{0.5}^{1.5} 4 t^2\,\text{d}t \\ =& \frac{4}{3}(1.5^3 - 0.5^3) = 4.33 \end{align}\]

Berechnungsvarianten

Wir betrachten Arbeitsintegrale in der \((x,y)\)-Ebene. Je nach Kurve kann das Arbeitsintegral auf verschiedene Arten berechnet werden.

• allgemein parametrisierte Kurve: \(s:\mathbb{R} \rightarrow \mathbb{R}^2: s(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix}\): allgemeinste Methode, siehe Beispiele oben, \(\text{d}x = x'(t)\,\text{d}t\) und \(\text{d}y = y'(t)\,\text{d}t\)

• Kurve, die sich nach \(x\) parametrisieren lässt: \(s:\mathbb{R} \rightarrow \mathbb{R}^2: s(x) = \begin{pmatrix} x \\ y(x) \end{pmatrix}\): \(\text{d}x = \text{d}x\) und \(\text{d}y = y'(x)\,\text{d}x\)

• horizontales Geradenstück auf Höhe \(y_0\): \(s:\mathbb{R} \rightarrow \mathbb{R}^2: s(x) = \begin{pmatrix} x \\ y_0 \end{pmatrix}\): \(\text{d}x = \text{d}x\) und \(\text{d}y = 0\)

• Kurve, die sich nach \(y\) parametrisieren lässt: \(s:\mathbb{R} \rightarrow \mathbb{R}^2: s(y) = \begin{pmatrix} x(y) \\ y \end{pmatrix}\): \(\text{d}x = x'(y)\,\text{d}y\) und \(\text{d}y = \text{d}y\)

• vertikales Geradenstück bei \(x_0\): \(s:\mathbb{R} \rightarrow \mathbb{R}^2: s(y) = \begin{pmatrix} x_0 \\ y \end{pmatrix}\): \(\text{d}x = 0\) und \(\text{d}y = \text{d}y\)

Weg(un)abhängigkeit

Nicht jedes Differential \(F_p (p,V)\,\text{d}p + F_V (p,V)\,\text{d}V\) bzw. \(F_x (x,y)\,\text{d}x + F_y (x,y)\,\text{d}y\) ist das vollständige Differential \(\text{d}f\) einer Funktion \(f(p,V)\) bzw. \(f(x,y)\). Insbesondere sind das Wärmedifferential \(T\,\text{d}S\) und das Arbeitsdifferential \(p\,\text{d}V\) keine Differentiale von Funktionen der Koordinaten \((p,V)\). In anderen Worten, es gibt Differentiale, die keine Stammfunktion besitzen!

• Differentiale, die das Differential einer Funktion \(f\) sind, heißen exakte Differentiale und werden mit dem Symbol d geschrieben: \(\text{d}f\). Das zugehörige Vektorfeld heißt konservativ und ist das Gradientenfeld \(\text{grad}(f)\) der Funktion \(f\).
• Differentiale, die keine Differentiale von Funktionen sind, heißen inexakte Differentiale und werden oft mit dem Symbol \(\delta\) geschrieben, um sie nicht mit exakten Differentialen zu verwechseln: \(\delta Q = T\,\text{d}S\), \(\delta W = p\,\text{d}V\). Das zugehörige Vektorfeld heißt nicht konservativ und ist kein Gradientenfeld.

Das Arbeitsintegral entlang einer Kurve von \(A\) nach \(B\) über ein exaktes Differential \(\text{d}f\) erfüllt

\[\int \text{d}f = f(B) - f(A).\]

Das Ergebnis ist also nur vom Anfangspunkt \(A\) und vom Endpunkt \(B\) der Kurve abhängig aber nicht vom Prozess dazwischen. Man sagt, dass ein solches Arbeitsintegral prozessunabhängig ist. Die Differenz \(f(B) - f(A)\) wird als \(\Delta f\) geschrieben: \(\Delta f = f(B) - f(A)\). Es folgt, dass das Arbeitsintegral über ein exaktes Differential entlang einer geschlossenen Kurve (Kreisprozess) ist Null.

Das Arbeitsintegral entlang eines Prozesses über ein inexaktes Differential wie z. B. \(\delta Q\) ist hingegen prozessabhängig. Die Wärme \(Q = \int\delta Q = \int T\,\text{d}S\) ist daher genauso wie die Arbeit \(W = \int\delta W = \int p\,\text{d}V\) abhängig vom Prozess zwischen dem Anfangszustand \(A\) und dem Endzustand \(B\). Daher macht es insbesondere keinen Sinn, von der Wärme oder der Arbeit des Gases in einem bestimmten Zustand zu sprechen. Man bezeichnet prozessabhängige Arbeitsintegrale als Prozessgrößen. Prozessunabhängige Arbeitsintegrale sind hingegen immer Änderungen von Zustandsgrößen, da diese Arbeitsintegrale als Integrale über Differentiale einer Funktion der Zustandskoordinaten, auch Zustandsfunktion genannt, geschrieben werden können.

Arbeitet man mit Vektorfeldern statt Differentialen, so ist das Arbeitsintegral entlang einer Kurve von \(A\) nach \(B\) über ein konservatives Vektorfeld \(\text{grad}(f)\) (und somit als Produkt über ein exaktes Differential) durch

\[\int \text{grad}(f) \cdot \text{d}s = f(B) - f(A) = \Delta f\]

gegeben. Das Ergebnis ist also wieder nur vom Anfangspunkt \(A\) und vom Endpunkt \(B\) der Kurve abhängig aber nicht vom Weg dazwischen. Man verwendet nun die Begriffe weg(un)abhängig statt prozess(un)abhängig und Skalarfeld oder Potential(funktion) statt Zustandsgröße oder Zustandsfunktion. Es folgt wieder, dass das Arbeitsintegral über ein konservatives Vektorfeld entlang einer geschlossenen Kurve (geschlossener Weg) ist Null.

Es gibt ein einfaches Kriterium, um bestimmen zu können, ob das Arbeitsintegral über ein Differential \(F_p (p,V)\,\text{d}p + F_V (p,V)\,\text{d}V\) oder ein Vektorfeld \(F=\begin{pmatrix} F_x (x,y) \\ F_y (x,y) \end{pmatrix}\) prozess(un)abhängig bzw. weg(un)abhängig ist.

Rotationskriterium:

• Differentiale: prozessunabhängig \(\Leftrightarrow\frac{\partial F_p}{\partial V} = \frac{\partial F_V}{\partial p}\), prozessabhängig \(\Leftrightarrow\frac{\partial F_p}{\partial V} \neq \frac{\partial F_V}{\partial p}\)
• Vektorfelder: wegunabhängig: \(\Leftrightarrow\text{rot}(F) = 0\), wegabhängig \(\Leftrightarrow\text{rot}(F) \neq 0\)

Es folgt, dass ein Gradientenfeld immer rotationsfrei ist: \(\text{rot}(\text{grad}(f)) = 0\).

Wir zeigen zuerst, dass das Wärmedifferential \(\delta Q\) und das Arbeitsdifferential \(\delta W\) inexakt sind:

• \(\delta Q = \frac{3}{2}V\,\text{d}p + \frac{5}{2}p\,\text{d}V\): \(\frac{3}{2} \neq \frac{5}{2}\)
• \(\delta W = p\,\text{d}V\): \(0 \neq 1\)

Nun subtrahieren wir die beiden inexakten Differentiale:

\[\begin{align} \delta Q - \delta W &= \frac{3}{2}V\,\text{d}p + \frac{5}{2}p\,\text{d}V - p\,\text{d}V \\ &= \frac{3}{2}V\,\text{d}p + \frac{3}{2}p\,\text{d}V \\ &= \text{d}(\frac{3}{2}pV) \\ &= \text{d}U \end{align}\]

Das Ergebnis ist das Differential der inneren Energie, also ein exaktes Differential. Dieser Zusammenhang zwischen der Änderung der inneren Energie des betrachteten Systems, aufgenommener Wärme und vom Systen geleisteter Arbeit ist der erste Hauptsatz der Thermodynamik: \(\text{d}U = \delta Q - \delta W\) bzw. nach Integration beider Seiten entlang eines beliebigen Prozesses: \(\Delta U = Q - W\).

Potentialfunktionen

Falls ein Differential exakt ist bzw. das zugehörige Vektorfeld konservativ ist, dann ist das betrachtete Differential das Differential \(\text{d}f\) einer Funktion \(f\) bzw. das Vektorfeld ist das Gradientenfeld \(\text{grad}(f)\) dieser Funktion, meist Potentialfunktion genannt. Aus \(\int \text{d}f = f(B) - f(A)\) folgt durch Umformen \(f(B) = \int \text{d}f + f(A)\). Der Wert der Potentialfunktion am Punkt \(B\) ist also durch das Arbeitsintegral von \(A\) nach \(B\) plus dem Wert der Potentialfunktion am Punkt \(A\) gegeben. Die Wahl des Prozesses bzw. Weges von \(A\) nach \(B\) ist irrelevant. Der Wert der Potentialfunktion am Punkt \(B\) ist bis auf die additive Konstante (Offset) \(f(A)\) eindeutig.

Beispiel:

Wir betrachten das Differential \((6xy + 1)\,\text{d}x + 3x^2\,\text{d}y\) und wählen die Punkte \(A=(0,0)\) und \(B=(x,y)\). Den Offset (=Integrationskonstante) \(f(A)\) setzen wir Null. Als Kurve von \(A=(0,0)\) nach \(B=(x,y)\) verwenden wir ein horizontales Geradenstück auf Höhe \(y=0\) von \((0,0)\) nach \((x,0)\) fortgesetzt mit einem vertikalen Geradenstück von \((x,0)\) nach \((x,y)\).

\[\begin{align} f(B) &= \int \text{d}f + f(A) \\ f(x,y) &= \int \text{d}f \\ &= \int_{(0,0)}^{(x,0)} (6xy + 1)\,\text{d}x + 3x^2\,\text{d}y + \int_{(x,0)}^{(x,y)} (6xy + 1)\,\text{d}x + 3x^2\,\text{d}y \\ &= x + 3x^2y \end{align}\]

Für den ersten Term des Integrals gilt \(\text{d}y=0\) und \(y=0\), für den zweiten Term gilt \(\text{d}x=0\) sowie \(x=x\).

Als Probe berechnen wir das Differential der Funktion \(f(x,y) = x + 3x^2y\) und erhalten \(\text{d}f = (6xy + 1)\,\text{d}x + 3x^2\,\text{d}y\).

Allgemeine gewöhnliche Differentialgleichungen

Themenüberblick:

• Beispiele
• Klassifizierung und Begriffe
• grafische Darstellung: Richtungsfeld, Integralkurve
• Lösungsmethoden: am computer und analytisch mit Trennung der Variablen und Integration exakter gewöhnlicher Differentialgleichungen

Beispiele

Newtonsche Bewegungsgleichung mit konstanter Kraft:

Auf einen Massenpunkt mit Masse \(m\), der sich entlang einer 1-dimensionalen Bahn (Straße, Schiene, Seilbahn etc.) mit Ortskoordinate \(x\) bewegen kann, wirke eine konstante Kraft \(F\) in Richtung der Bahn. Seine Bewegung wird durch eine Funktion \(x(t)\) beschrieben, die jedem Zeitpunkt \(t\) den (Aufenthalts-)Ort \(x(t)\) zuordnet. Die Newtonsche Bewegungsgleichung (Newtons zweites Gesetz) besagt, dass die Ortsfunktion \(x(t)\) die folgende Gleichung, genannt Bewegungsgleichung, erfüllt

\[m\ddot{x}(t) = F.\]

Mit dem Lösen der Bewegungsgleichung ist das Bestimmen jener Funktion(en) \(x(t)\) gemeint, die die Bewegungsgleichung und evtl. zusätzliche Bedingungen (Anfangs- oder Randbedingungen) erfüllen. Da in der Bewegungsgleichung Ableitungen der gesuchten Funktion \(x(t)\) vorkommen, ist sie ein Beispiel für eine Differentialgleichung (DGL). Weil die höchste vorkommende Ableitung die zweite zeitliche Ableitung der Ortskoordinate \(x\) ist (\(\ddot{x}\)), sprechen wir von einer Differentialgleichung 2. Ordnung.

Lösung:

• allgemeine Lösung: durch zweimaliges Integrieren erhält man \(x(t) = \frac{F}{2m}t^2 + C_1 t + C_2\) mit Integrationskonstanten \(C_1\) und \(C_2\)
• partikuläre Lösung für Anfangsbedingungen \(x(0)=2\) (Anfangsort) und \(\dot{x}(0)=5\) (Anfangsgeschwindigkeit): \(x(t) = \frac{F}{2m}t^2 + 5 t + 2\)

Newtonsche Bewegungsgleichung mit linearer Rückstellkraft:

• Bewegungsgleichung: \(m\ddot{x}(t) = -kx(t)\), Federkonstante \(k>0\)
• allgemeine Lösung: Definiere den Parameter \(\omega:=\sqrt{\frac{k}{m}}\). Dann ist die allgemeine Lösung durch \(x(t) = C_1 \cos(\omega t) + C_2 \sin(\omega t)\) gegeben.

Newtons Abkühlgesetz:

Wir suchen die Temperatur \(T_W(t)\) einer Tasse Glühwein als Funktion der Zeit \(t\). Der Glühwein befindet sich in einer Umgebung mit konstanter Umgebungstemperatur \(T_U\). Newtons Abkühlgesetz besagt, dass der Energieverlust pro Zeit durch Wärmeübertragung an die Umgebung, geschrieben als \(\dot{Q}(t)\), die Gleichung

\[\dot{Q}(t) = -d [T_W(t) - T_U]\]

mit einer positiven Konstante \(d\) (Abkühlkoeffizient) erfüllt. Aus \(\dot{Q}(t) = c \cdot m \cdot \dot{T}_W(t)\) (\(m\) die Masse des Glühweins, \(c\) seine spezifische Wärmekapazität) folgt

\[cm\dot{T}_W(t) = -d [T_W(t) - T_U]\]

als Differentialgleichung für die Temperatur \(T_W(t)\).

Wir führen die Temperaturdifferenz zur Umgebung als neue abhängige Variable ein: \(\Delta T(t) := T_W(t) - T_U\), und beachten, dass \(\text{d}{\Delta T}/\text{d}t = \dot{T}_W(t)\) gilt. Dadurch erhalten wir die kompaktere Differentialgleichung

\[\dot{T}(t) = -\lambda T(t)\]

mit dem einzigen Parameter \(\lambda=\frac{d}{cm}\), der den Zeitverlauf bestimmt.

Lösung: \(T(t) = T(0)e^{-\lambda t}\), d. h. die Temperaturdifferenz zur Umgebung klingt exponentiell vom Anfangswert \(T(0)\) ab. Je größer \(\lambda\) ist, umso schneller kühlt der Glühwein aus.

Wärmeleitungsgleichung:

Wir betrachten einen isolierten Metallstab mit Orstkoordinate \(x\) und Temperaturverteilung \(T_0(x)\) zum Anfangszeitpunkt \(t=0\). Gesucht ist die daraus resultierende Temperaturverteilung zu späteren Zeitpunkten \(t\) an jedem betrachteten Ort \(x\), also eine Funktion \(T(x,t)\), die \(T(x,0) = T_0(x)\) erfüllt. Die Dynamik (=zeitliche Entwicklung) wird durch die Wärmeleitungsgleichung

\[\frac{\partial T}{\partial t} = a\frac{\partial^2 T}{\partial x^2}\]

beschrieben. Diese ist eine sogenannte partielle Differentialgleichung. Der Parameter \(a>0\) bezeichnet die Temperaturleitfähigkeit des Metallstabs. Die Wärmeleitungsgleichung besagt z. B., dass die zweite Ableitung (Krümmung) nach dem Ort zu einer zeitlichen Temperaturänderung führt:

• Falls \(\frac{\partial^2 T}{\partial x^2}(x,t) > 0\), dann ist zum Zeitpunkt \(t\) die Temperatur in der Umgebung von \(x\) größer als bei \(x\), und die Temperatur steigt mit der Zeit an: \(\frac{\partial T}{\partial t} > 0\).
• Falls \(\frac{\partial^2 T}{\partial x^2}(x,t) < 0\), dann ist zum Zeitpunkt \(t\) die Temperatur in der Umgebung von \(x\) kleiner als bei \(x\), und die Temperatur fällt mit der Zeit ab: \(\frac{\partial T}{\partial t} < 0\).

In drei Raumdimensionen wird eine Funktion \(T(x,y,z,t)\) gesucht, die die Wärmeleitungsgleichung

\[\frac{\partial T}{\partial t} = a\left[\frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2}\right] = a\Delta T\]

erfüllt. Der Operator \(\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\) ist der sogenannte Laplace-Operator (nicht zu verwechseln mit dem Nabla-Operator). Aus dem Gradienten von \(T(x,y,z,t)\) bezüglich den drei kartesichen Raumkoordinaten kann man die Wärmestromdichte \(\dot{q}\) (z. B. in Watt pro Quadratmeter) an jedem Ort und zu jedem Zeitpunkt bestimmen:

\[\dot{q} = -\lambda \nabla T.\]

Der Parameter \(\lambda\) bezeichnet die Wärmeleitfähigkeit.

Klassifizierung und Begriffe

Eine gewöhnliche Differentialgleichung (GDGL, englisch ordinary differential equation (ODE)) beschreibt das Verhalten einer Funktion, die von einer einzigen Variablen abhängt. Eine partielle Differentialgleichung (PDGL, englisch partial differential equation (PDE)) beschreibt das Verhalten einer Funktion, die von mehr als einer Variablen abhängt.

Lineare Differentialgleichungen enthalten nur lineare Terme der gesuchten Funktion und ihrer (partiellen) Ableitungen. Alle anderen Differentialgleichungen heißen nicht-lineare Differentialgleichungen.

Beispiele:

• \(y'(x) = xy(x) + 1\) oder kürzer \(y' = xy + 1\) ist linear
• \(y'' + xy + y^2=0\) ist nicht-linear
• \(\frac{\text{d}y}{\text{d}x} = -\frac{x}{y}\) ist nicht-linear
• \(x^3\frac{\text{d}y}{\text{d}x} + \sin(x) y = e^x\) ist linear

Die Ordnung der höchsten vorkommenden (partiellen) Ableitung bezeichnet die Ordnung einer DGL.

Beispiele:

• \(y' = xy + 1\) ist von 1. Ordnung
• \(y'' + xy + y^2=0\) ist von 2. Ordnung
• \(\frac{\partial T}{\partial t} = a\frac{\partial^2 T}{\partial x^2}\) ist von 2. Ordnung

Die allgemeine Lösung einer GDGL enthält eine oder mehrere Integrationskonstanten, deren Werte durch Vorgaben von Anfangs- und/oder Randbedingungen bestimmt werden können. Eine partikuläre Lösung enthält keine unbestimmten Integrationskonstanten.

Das Paket aus GDGL + Anfangs- und/oder Randbedingungen heißt Anfangs- bzw. Randwertproblem. Seine Lösung liefert die zugehörige eindeutige partikulare Lösung, sofern die Anfangs- und/oder Randbedingungen dafür ausreichend und nicht überbestimmend sind.

Grafische Darstellung

Eine GDGL erster Ordnung für die gesuchte Funktion \(y(x)\) ist von der Form

\[y'(x) = f(x,y(x)).\]

Dabei ist \(f\) eine vorgegebene Funktion, die die Steigung \(y'(x)\) von \(y(x)\) an jedem Punkt in der \((x,y)\)-Ebene angibt.

Beispiele:

• \(y'(x) = x + y^2(x) \quad\Rightarrow\quad f(x,y) = x + y^2\)
• \(y'(x) = xy(x) \quad\Rightarrow\quad f(x,y) = xy\)

Wir können alternativ die Ableitung \(y'(x)\) als \(\frac{\text{d}y}{\text{d}x}\) schreiben und erhalten nach Multiplikation mit \({\text{d}x}\) die Differential-Gleichung

\[\text{d}y = f(x,y(x))\,{\text{d}x}.\]

An jedem Punkt der \((x,y)\)-Ebene wird dadurch ein Verhältnis zwischen der \(x\)-Änderung \(\text{d}x\) und der \(y\)-Änderung \(\text{d}y\) vorgeschrieben, das durch die Tangenten an die Lösung \(y(x)\) erfüllt werden muss.

Das Skalarfeld \(f(x,y)\) gibt somit an jedem Punkt \((x,y)\) eine Steigung bzw. Richtung vor und wird als Richtungsfeld der zugehörigen GDGL bezeichnet.

Die Lösung einer GDGL heißt auch Integralkurve.

Beispiel exponentielles Wachstum/Zerfall: Für eine Konstante \(a\) betrachten wir die GDGL \(y' = ay.\) Das Richtungsfeld \(f(x,y)=ay\) hängt nur von \(y\) ab. Die Integralkurven sind \(y(x)= Ce^{ax}\) mit der Integrationskonstanten \(C\), die gleich dem Anfangswert \(y(0)\) ist.

Code

a = 0.10
x = np.arange(-2, 8, 0.5)
y = np.arange(-5, 5, 0.5)
X, Y = np.meshgrid(x, y)

dX = np.ones(X.shape)
dY = a*Y

# zwei Integralkurven
C_1 = 1.5
y_lsg_1 = C_1*np.exp(a*x)
C_2 = -2
y_lsg_2 = C_2*np.exp(a*x)


plt.figure()
plt.quiver(X, Y, dX, dY, headwidth=0.0, scale = 20, pivot='middle', label='Richtungsfeld')
plt.plot(x, y_lsg_1, label='Lösung 1 (Anfangswert 1.5)')
plt.plot(x, y_lsg_2, label='Lösung 2 (Anfangswert 2.5)')
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
plt.legend(loc='best')
plt.grid(True)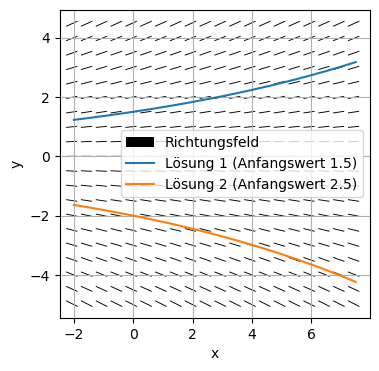

Lösungsmethoden

Übersicht:

• Lösung am Computer
  • numerisch
  • symbolisch
• Analytische Lösungsmethoden, die wir behandeln:
  • Trennung der Variablen
  • exakte Differentialgleichungen

Numerische Lösung: z. B. mit der SciPy-Funktion odeint

Code

from scipy.integrate import odeint

Für eine Konstante \(a\) und Anfangsbedingung \(y(0)=y_0\) lösen wir die GDGL \(y' = ay.\)

Code

# Definition der Ableitungsfunktion:
def fun(y, x): # Achtung! Die Reihenfolge der Argumente muss (y, x) sein.
    return a*y

# A sequence of time points for which to solve for y. 
# The initial value point should be the first element of this sequence.
x = np.arange(0, 8, 0.5) 

# The initial value:
y0 = -1.5  

# Solve numerically with odeint:
y_num = odeint(fun, y0, x)

# Vergleich mit analytischer Lösung:
y_lsg = y0*np.exp(a*x)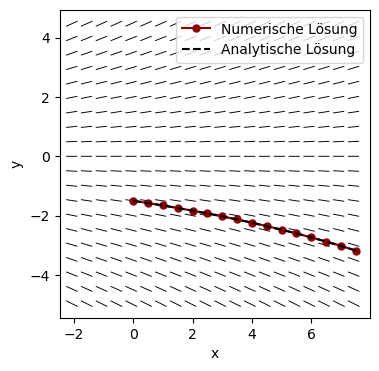

Code

plt.figure()

plt.quiver(X, Y, dX, dY, headwidth=0.0, scale = 20, pivot='middle')
plt.plot(x, y_num, '-o',ms=5,color='darkred', label='Numerische Lösung')
plt.plot(x, y_lsg, ls='--', color='black', label='Analytische Lösung')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=1)
plt.axis('equal');

Analytische Lösung: Trennung der Variablen:

Diese Methode setzt voraus, dass sich in einer GDGL \(y' = f(x,y)\) nach Umformen zu \(\text{d}y = f(x,y)\,{\text{d}x}\) die Variablen \(y\) und \(x\) auf je eine Gleichungsseite trennen lassen. Anschließend kann jede Seite über ihre Variable integriert werden.

Beispiel 1:

\[\begin{align} y' &= 2y \\ \text{d}y &= 2y\,\text{d}x \\ \frac{1}{y}\text{d}y &= 2\,\text{d}x \\ \int\frac{1}{y}\text{d}y &= \int 2\,\text{d}x \\ \ln|y|&= 2x + C \\ |y| &= e^{C + 2x} \\ y &= \pm e^{C}e^{2x} \\ y &= y(0)e^{2x} \end{align}\]

Hier ist der Fall \(y(0)=0\) ausgeschlossen.

Beispiel 2:

Die GDGL \(3y' + y^4\cos(x)=0\) mit Anfangsbedingung \(y(\frac{\pi}{2})=\frac{1}{2}\) kann durch Trennung der Variablen gelöst werden.

Ergebnis: \[y(x) = \dfrac{1}{\sqrt[3]{\sin(x) + 7}}\]

Exakte Gewöhnliche Differentialgleichungen:

Diese Methode setzt voraus, dass eine GDGL \(y' = f(x,y)\) nach Umformen zu \(\text{d}y - f(x,y)\,{\text{d}x} = 0\) einem exakten Differential \(\text{d}y - f(x,y)\,{\text{d}x}\) entspricht. Dann ist nämlich die Bedingung \(\text{d}y - f(x,y)\,{\text{d}x} = 0\) gleichbedeutend mit \(\text{d}F = 0\) für eine zu findende Funktion \(F(x,y).\) Die Integralkurven der GDGL sind die Konturlinien von \(F\), weil sich entlang dieser \(F\) nicht ändert, also \(\text{d}F\) gleich Null ist.

Beispiel 1: In der GDGL \(\dot{y}=\frac{2t + y}{y - t}\) lassen sich die Variablen nicht trennen. Sie ist aber eine exakte GDGL.

\[\begin{align} \dot{y} &= \frac{2t + y}{y - t} \\ (y - t)\,\text{d}y &= (2t + y)\,\text{d}t \\ (2t + y)\,\text{d}t + (t - y)\,\text{d}y &= 0 \end{align}\]

Code

# Richtungsfeld:

t = np.arange(-3.25, 3.25, 0.5)
y = np.arange(-3.00, 3.00, 0.5)
T, Y = np.meshgrid(t, y)
dT = (  Y - T)/np.sqrt( (Y - T)**2 + (2*T + Y)**2 )
dY = (2*T + Y)/np.sqrt( (Y - T)**2 + (2*T + Y)**2 )

plt.figure()
plt.quiver(T, Y, dT, dY, headwidth=0.0, scale = 10, pivot='middle')
plt.xlabel('t')
plt.ylabel('y')
plt.grid(False)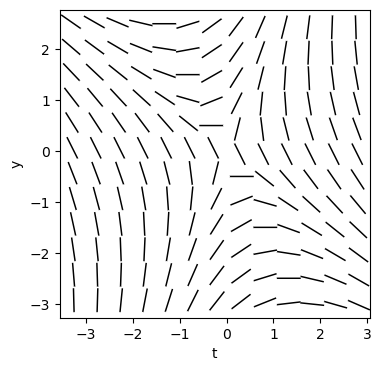

Das Differential \((2t + y)\,\text{d}t + (t - y)\,\text{d}y\) ist exakt, was mit dem Rotationskriterium nachgeprüft werden kann:

\[\begin{pmatrix}\frac{\partial}{\partial t} \\ \frac{\partial}{\partial y}\end{pmatrix} \times \begin{pmatrix} 2t + y \\ t - y \end{pmatrix} = 1 - 1 = 0.\]

Daher gibt es eine Funktion \(F(t,y)\) mit \(\text{d}F = (2t + y)\,\text{d}t + (t - y)\,\text{d}y.\) Durch ein Wegintegral von z. B. \((0,0)\) nach \((t,y)\) über einen rechteckigen Weg erhalten wir \(F(t,y) = t^2 + yt - \frac{y^2}{2} + C\) mit \(C\) einer Integrationskonstanten:

\[\begin{align} F(t,y) &= \int_{(0,0)}^{(t,y)} \text{d}F \\ &= \int_{(0,0)}^{(t,y)} (2t + y)\,\text{d}t + (t - y)\,\text{d}y \\ &= \int_{(0,0)}^{(t,0)} (2t + y)\,\text{d}t + (t - y)\,\text{d}y + \int_{(t,0)}^{(t,y)} (2t + y)\,\text{d}t + (t - y)\,\text{d}y \\ &= \int_0^t (2t + 0)\,\text{d}t + \int_0^y (t - y)\,\text{d}y \\ &= t^2 \Big|_{t=0}^{t=t} + (ty -\frac{y^2}{2})\Big|_{y=0}^{y=y} + C\\ &= t^2 + ty -\frac{y^2}{2} + C \end{align}\]

Code

# Richtungsfeld:
t = np.arange(-3.25, 3.25, 0.5)
y = np.arange(-3.00, 3.00, 0.5)
T, Y = np.meshgrid(t, y)
dT = (  Y - T)/np.sqrt( (Y - T)**2 + (2*T + Y)**2 )
dY = (2*T + Y)/np.sqrt( (Y - T)**2 + (2*T + Y)**2 )

plt.figure()
plt.quiver(T, Y, dT, dY, headwidth=0.0, scale = 10, pivot='middle')

# Konturlinien von F(t,y):
t = np.arange(-3.25, 3.25, 0.05)
y = np.arange(-3.00, 3.00, 0.05)
T, Y = np.meshgrid(t, y)
F = T**2 + T*Y - 1/2*Y**2

plt.contour(T, Y, F, 15, cmap= 'Reds')

plt.xlabel('t')
plt.ylabel('y')
plt.grid(False)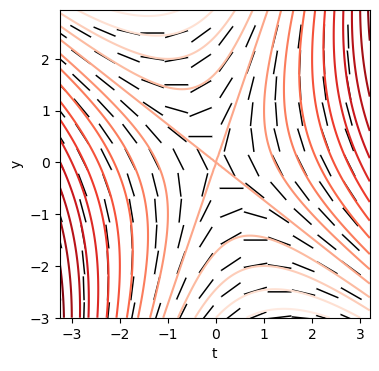

Die Konturlinien von \(F\) und somit die Lösungen der GDGL sind gegeben durch \(y(t) = t \pm \sqrt{3t^2 + D}\) für konstante Werte von \(D\):

Nachdem für das vollständige Differential \(dF=0\) gilt, muss die Funktion \(F\) einer Konstanten \(\tilde{C}\) entsprechen, die beim Ableiten wieder verschwindet.

\[\begin{align} t^2 + ty -\frac{y^2}{2} + C &= \tilde{C} \\ y^2 - 2ty - 2t^2 - 2[C - \tilde{C}] &= 0 \\ y(t) &= t \pm \sqrt{t^2 + 2t^2 + 2[C - \tilde{C}]} \\ y(t) &= t \pm \sqrt{3t^2 + D} \end{align}\]

Beispiel 2: 1-dimensionaler Massenpunkt in einem ortsabhängigen Kraftfeld: Die Bewegungsgleichung \(m\ddot{x}=F(x)\) ist eine GDGL zweiter Ordnung. Durch das Einführen der zusätzlichen Funktion \(v(t)\) (Geschwindigkeit) können wir die Bewegungsgleichung zu zwei GDGL erster Ordnung umformen.

\[\begin{align} \dot{x}=v &\quad m\dot{v}=F(x) \\ \text{d}x = v\,\text{d}t &\quad m\,\text{d}v = F(x)\,\text{d}t \end{align}\]

Nach Multiplizieren von \(m\,\text{d}v = F(x)\,\text{d}t\) mit \(v\) und Ersetzen von \(v\,\text{d}t\) auf der rechten Seite durch \(\text{d}x\) erhalten wir

\[\begin{align} mv\,\text{d}v &= F(x)\,\text{d}x \\ mv\,\text{d}v - F(x)\,\text{d}x &= 0 \end{align}\]

Dies ist eine exakte GDGL, da

\[\begin{pmatrix}\frac{\partial}{\partial v} \\ \frac{\partial}{\partial x}\end{pmatrix} \times \begin{pmatrix} mv \\ -F(x) \end{pmatrix} = 0 - 0 = 0.\]

Eine Stammfunktion \(-U(x)\) von \(F(x)\) heißt in der Physik potentielle Energie der Kraft \(F(x)\) und erfüllt also \(F(x)=-U'(x)\). Mit ihr erhalten wir

\[\begin{align} \text{d}\left(m\frac{v^2}{2}\right) - \text{d}\left(-U(x)\right) &= 0 \\ \text{d}\left(m\frac{v^2}{2} + U(x)\right) &= 0 \end{align}\]

Die Lösungen der Bewegungsgleichungen sind somit Konturlinien der Funktion

\[E(x, v) = m\frac{v^2}{2} + U(x),\]

die als Gesamtenergie des Massenpunktes am Ort \(x\) mit Geschwindigkeit \(v\) bezeichnet wird. Entlang jeder Integralkurve der Bewegungsgleichung ist also die Gesamtenergie erhalten: \(m\frac{v(t)^2}{2} + U(x((t)) = E_0\) für eine konstante \(E_0\) wie Energie.

Beispiel: Die lineare Rückstellkraft \(F(x) = -kx\) mit Federkonstante \(k>0\) hat die potentielle Energie \(U(x)=\frac{k}{2}x^2\). Die Gesamtenergie lautet \(E(x, v) = m\frac{v^2}{2} + k\frac{x^2}{2}\), deren Konturlinien Ellipsen im Phasenraum (=Ort-Geschwindigkeits-Diagramm) sind.

Code

# Konturlinien von E(x,v): 

m = 3
k = 1

x = np.arange(-3, 3, 0.1)
v = np.arange(-3, 3, 0.1)
X, V = np.meshgrid(x, v)
E = 0.5*m*V**2 + 0.5*k*X**2

plt.figure(figsize=(4,4))
plt.contour(X, V, E, np.linspace(0,20, num=25), cmap= 'coolwarm')
plt.xlabel('x')
plt.ylabel('v')
plt.grid(True)

Lineare gewöhnliche Differentialgleichungen 1. Ordnung

Themenüberblick:

• konstante Koeffizienten: allgemeine Lösung, Beispiele und Anwendungen
• allgemeine Koeffizientenfunktionen: allgemeine Lösung, Beispiele und Anwendungen

Konstante Koeffizienten

Eine lineare GDGL 1. Ordnung mit konstanten Koeffizienten \(a\) und \(b\) hat die Gleichung

\[\boxed{\dot{y} + ay = b}.\]

Allgemeine Lösung:

Der uninteressantere Fall \(a=0\) hat die Lösung \(y(t) = bt + C\) mit der Integrationskonstanten \(C\). Im Folgenden betrachten wir den interessanteren Fall \(a\neq0\):

Wir überprüfen, ob die DGL \(\dot{y} + ay = b\) exakt ist, und schreiben sie dafür zu

\[\text{d}y + (ay-b)\,\text{d}t =0\]

um. Das Rotationskriterium liefert

\[\begin{pmatrix} \frac{\partial}{\partial y} \\ \frac{\partial}{\partial t}\end{pmatrix}\times\begin{pmatrix} 1\\ay - b \end{pmatrix}=a-0=a.\]

Die DGL ist also nicht exakt, da wir \(a\neq 0\) annehmen.

Herausheben von \((ay - b)\) aus \(\text{d}y + (ay-b)\,\text{d}t =0\) liefert

\[(ay-b)\left[ \frac{1}{ay-b}\,\text{d}y + \text{d}t\right] = 0.\]

Wenn der erste Faktor \(ay-b\) Null ist, erhalten wir die konstante Lösung \(y(t) = \frac{b}{a}\), deren Ableitung \(\dot{y}(t)\) Null ist. Daher wird diese Lösung als steady state Lösung bezeichnet. Null-Setzen des zweiten Faktors \(\frac{1}{ay-b}\,\text{d}y + \text{d}t\) liefert nun eine exakte DGL, da

\[\begin{pmatrix} \frac{\partial}{\partial y} \\ \frac{\partial}{\partial t}\end{pmatrix}\times\begin{pmatrix} \frac{1}{ay-b} \\ 1 \end{pmatrix}= 0 - 0 = 0.\]

Ihre Lösung lautet \(y(t)= Ce^{-at} + \frac{b}{a}\) für \(C\neq 0\), denn:

\[\begin{align} \frac{1}{ay - b}\text{d}y + \text{d}t &= 0 \\ \text{d} \left(\frac{1}{a} \ln|ay - b| + t \right) &= 0 \\ \frac{1}{a} \ln|ay - b| + t &= C_1 \\ \ln|ay - b| &= C_2 - at \\ |ay - b| &= e^{C_2} e^{-at} \\ ay - b &= \pm e^{C_2} e^{-at} \\ ay - b &= C_3 e^{-at} \\ y(t) &= C e^{-at} + \frac{b}{a} \end{align}\]

Insgesamt lautet die allgemeine Lösung \(y(t)= Ce^{-at} + \frac{b}{a}\), wobei \(C\) auch Null sein kann und dem Anfangswert \(y(0)\) minus \(\frac{b}{a}\) entspricht:

\[\boxed{y(t)= \left(y(0)- \frac{b}{a}\right)e^{-at} + \frac{b}{a}}\]

Wir schreiben dieses Ergebnis zusätzlich in der alternativen Form:

\[\boxed{y(t)= y(0)e^{-at} + \frac{b}{a}\left( 1 - e^{-at} \right)}\]

• Falls \(a<0\) ist, divergiert \(y(t)\), ausser \(y(0)=\frac{b}{a}\).
• Falls \(a>0\) ist, konvergiert \(y(t)\) vom Anfangswert \(y(0)\) zum steady state Wert \(\frac{b}{a}\). Der Anteil \(y(0)e^{-at}\) beginnt bei \(y(0)\) und geht gegen Null. Der Anteil \(\frac{b}{a}\left( 1 - e^{-at} \right)\) beginnt bei Null und geht gegen \(\frac{b}{a}\).

Beispiele und Anwendungen:

Elektrischer Schaltkreis: Der Strom \(I(t)\) als Funktion der Zeit \(t\) erfüllt in einem elektrischen Schaltkreis mit vorgegebener konstanter Spannung \(U\) und in Serie geschaltetem ohmschen Widerstand \(R\) und Induktivität \(L\) die DGL

\[L\dot{I} + RI = U.\]

Nach Umformen zu \(\dot{I} + \frac{R}{L}I = \frac{U}{L}\) können wir die Lösungsformel verwenden. Die Lösung lautet

\[I(t)= I(0)e^{-\frac{R}{L}t} + \frac{U}{R}\left(1 - e^{-\frac{R}{L}t}\right).\]

Der Strom konvergiert zum steady state Wert \(\frac{U}{R}\).

Verschmutztes Wasser: Ein See enthält \(4\cdot10^7\) Liter reines Wasser zum Zeitpunkt \(t=0\). Anschließend fließt verschmutztes Wasser in den See, das 0.67 Liter Schadstoff und 10 Liter reines Wasser pro Sekunde in den See bringt. Wir nehmen an, dass sich das eingebrachte verschmutzte Wasser sofort mit dem Seewasser vermischt. Pro Sekunde fließen 10.67 Liter aus dem See hinaus. Wir bestimmen die Menge an Schadstoff im See als Funktion der Zeit. Mit \(y(t)\) bezeichnen wir die Liter Schadstoff für Zeitpunkte \(t\geq 0\). Der Anteil an Schadstoff pro Liter Seewasser beträgt \(\frac{y(t)}{4\cdot10^7}\).

• Aufstellen der DGL: Die Änderung der Schadstoffmenge im See ist gleich der Abflussmenge an Schadstoff pro Zeit plus der Einflußmenge pro Zeit, d. h. \(\dot{y} = -10.67\frac{y}{4\cdot10^7} + 0.67\). Die Terme der DGL haben die Einheit Liter pro Sekunde.
• Lösung: \(y(t) = \frac{0.67}{10.67}4\cdot10^7(1 - e^{-\frac{10.67}{4\cdot10^7}t})\)
• Der steady state der Schadstoffmenge \(y(t)\) ist \(\frac{0.67}{10.67}4\cdot10^7 \approx 2.51\cdot10^6\).
• Der steady state der Schadstoffkonzentration \(\frac{y(t)}{4\cdot10^7}\) ist \(\frac{0.67}{10.67} \approx 0.063\).

Wann werden 90 % des steady states erreicht? Antwort: nach ca. 100 Tagen:

\[\begin{align} 1 - e^{-\frac{10.67}{4\cdot10^7}t} &= 0.9 \\ e^{-\frac{10.67}{4\cdot10^7}t} &= 0.1 \\ -\frac{10.67}{4\cdot10^7}t &= \ln(0.1) \\ t &= 862314\,\text{Sekunden} \approx 100\,\text{Tage} \end{align}\]

Code

a = 10.67/4e7
b = 0.67
y0 = 0
t = np.linspace(0,365) # Tage
y = ((y0 - b/a)*np.exp(-a*24*60*60*t) + b/a)/4e7*100  # Konzentration in %
y_steady_state = b/a/4e7*100*np.ones(np.shape(t))  # steady state Konzentration in %

plt.figure(figsize=(5,3))
plt.plot(t, y, color='darkred',label='Zeitverlauf')
plt.plot(t, y_steady_state, '--',color='black', label='steady state')
plt.xlabel('Tage')
plt.ylabel('Konzentration (%)')
plt.legend(loc='best')
plt.grid(True)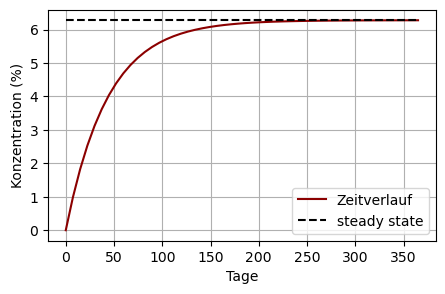

Raumtemperatur: Um Mitternacht beträgt die Raumtemperatur in der FH Vorarlberg 20 °C und außen -5 °C. Die Heizung fällt aus. Zwei Stunden später beträgt die Raumtemperatur nur noch 10 °C. Die Außentemperatur bleibt konstant auf -5 °C. Wir bestimmen den Zeitverlauf der Raumtemperatur.

Dazu verwenden wir \(T(t)\) für die Raumtemperatur zum Zeitpunkt \(t\) und \(T_A\) für die Außentemperatur. Newtons Abkühlgesetz besagt, dass \(\dot{T}(t) = -\lambda (T(t) - T_A)\). Wir wissen, dass \(T(0)=20\) und \(T_A=-5\), aber der Parameter \(\lambda\) ist vorerst unbekannt. Die Parameter \(a\) und \(b\) der allgemeinen Form \(\dot{y} + ay = b\) identifizieren wir als \(a=\lambda\) und \(b = \lambda T_A\). Daher lautet die allgemeine Lösung

\[T(t) = \left( T(0)- T_A \right) e^{-\lambda t} + T_A.\]

Aus der Bedingung \(T(2)=10\) können wir \(\lambda\) bestimmen:

\[\begin{align} 10 &= (20 + 5) e^{-\lambda 2} - 5 \\ 15 &= 25e^{-\lambda 2} \\ e^{-\lambda 2} &= 0.6 \\ -\lambda 2&= \ln(0.6) \\ \lambda &= -0.5\ln(0.6) \approx 0.2554 \end{align}\]

Code

a = -0.5*np.log(0.6)
b = -0.5*np.log(0.6)*(-5)
T0 = 20
t = np.linspace(0, 24) # Stunden
T = (T0 - b/a)*np.exp(-a*t) + b/a
T_steady_state = b/a*np.ones(np.shape(t))

plt.figure(figsize=(5,3))
plt.plot(t, T, color='darkred',label='Raumtemperatur')
plt.plot(t, T_steady_state, '--', color='black', label='steady state = Aussentemperatur')
plt.xlabel('Stunde nach Mitternacht')
plt.ylabel('Temperatur (°C)')
plt.legend(loc='best')
plt.ylim(-10, 22)
plt.grid(True)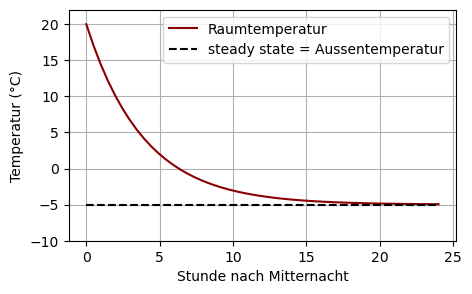

Wann beträgt die Raumtemperatur nur noch 5 °C?

\[\begin{align} 5 &= 25e^{-\lambda t} - 5 \\ 10 &= 25e^{-\lambda t} \\ e^{-\lambda t} &= 0.4 \\ -\lambda t &= \ln(0.4) \\ t &= -\frac{\ln(0.4)}{\lambda} \approx 3.587 \end{align}\]

Antwort: ca. 3.6 Stunden nach Mitternacht.

Allgemeine Koeffizientenfunktionen

Eine lineare GDGL 1. Ordnung mit Koeffizientenfunktionen \(a(t)\) und \(b(t)\) hat die Gleichung

\[\boxed{\dot{y} + a(t)y = b(t)}.\]

Allgemeine Lösung:

Der uninteressantere Fall \(a(t)=0\) hat die Lösung \(y(t) = B(t) + C\) mit \(B(t)\) einer Stammfunktion von \(b(t)\) und einer Integrationskonstanten \(C\). Im Folgenden betrachten wir den interessanteren Fall \(a(t)\neq0\), d. h. die Funktion \(a(t)\) ist nicht zu allen Zeitpunkten \(t\) gleich Null:

Wir überprüfen, ob die DGL exakt ist, und schreiben sie dafür zu

\[\text{d}y + \left[a(t)y - b(t)\right]\text{d}t = 0\]

um. Das Rotationskriterium liefert

\[\begin{pmatrix} \frac{\partial}{\partial y} \\ \frac{\partial}{\partial t}\end{pmatrix}\times\begin{pmatrix} 1\\a(t)y - b(t) \end{pmatrix}=a(t) - 0 = a(t).\]

Die DGL ist nicht exakt, da wir \(a(t)\neq 0\) annehmen.

Wir multiplizieren \(\text{d}y + \left[a(t)y - b(t)\right]\text{d}t =0\) mit dem integrierenden Faktor \(e^{A(t)}\), wobei \(A(t)\) eine Stammfunktion von \(a(t)\) ist. Die resultierende DGL \(e^{A(t)}\text{d}y + e^{A(t)}\left[a(t)y - b(t)\right]\text{d}t =0\) ist exakt. Wir lösen sie in den folgenden (zugegeben nicht sehr offensichtlichen) Schritten

\[\begin{align} e^{A(t)}\text{d}y + e^{A(t)}\left[a(t)y - b(t)\right]\text{d}t &= 0 \\ e^{A(t)}\text{d}y + e^{A(t)}a(t)y\,\text{d}t &= e^{A(t)}b(t)\,\text{d}t \\ \text{d}\left( e^{A(t)}y\right) &= e^{A(t)}b(t)\,\text{d}t \\ \int\text{d}\left( e^{A(t)}y\right) &= \int e^{A(t)}b(t)\,\text{d}t + C \\ e^{A(t)}y &= \int e^{A(t)}b(t)\,\text{d}t + C \\ y &= e^{-A(t)} \left[ \int e^{A(t)}b(t)\,\text{d}t + C \right] \end{align}\]

Die allgemeine Lösung mit Integrationskonstante \(C\) lautet also

\[\boxed{y(t) = e^{-A(t)} \left[ \int e^{A(t)}b(t)\,\text{d}t + C \right]}.\]

Diese Formel liefert auch für den Fall \(a(t)=0\) die Lösung, allerdings auf eine umständliche Art.

Beispiel und Anwendung:

Der Strom \(I(t)\) als Funktion der Zeit \(t\) erfüllt in einem elektrischen Schaltkreis mit vorgegebener zeitabhängiger Spannung \(U(t) = U_0 \sin(\omega t)\) und in Serie geschaltetem ohmschen Widerstand \(R\) und Induktivität \(L\) die DGL

\[L\dot{I} + RI = U_0 \sin(\omega t).\]

Nach Division durch \(L\) erhalten wir die DGL

\[\dot{I} + \frac{R}{L}I = \frac{U_0}{L} \sin(\omega t),\]

sodass wir folgende Identifikationen mit der allgemeinen Form \(\dot{y} + a(t)y = b(t)\) machen können:

• \(a(t) = \frac{R}{L}\)
• \(b(t) = \frac{U_0}{L} \sin(\omega t)\)

Mit Hilfe der Integralformel

\[\int e^{rt}\sin(st)\,\text{d}t = \frac{1}{r^2 + s^2}e^{rt}\left[ r\sin(st) - s\cos(st) \right]\]

für Konstanten \(a\) und \(b\) läßt sich die Lösung der DGL mit der Lösungsformel bestimmen:

\[I(t) = \frac{U_0}{L}\frac{1}{(R/L)^2 + \omega^2}\left( \frac{R}{L}\sin(\omega t) - \omega\cos(\omega t) \right) + Ce^{-\frac{R}{L}t}.\]

Lineare gewöhnliche Differentialgleichungen 2. Ordnung

Themenüberblick:

• Lösungsstruktur: homogene (Exponentialansatz) und partikuläre Lösungen, allgemeine Lösung, Anfangswertproblem
• Übungsbeispiele

Lösungsstruktur

Homogen mit konstanten Koeffizienten:

Die allgemeine Lösung der homogenen linearen Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten

\[\ddot{y}(t) + a \dot{y}(t) + by(t) = 0\]

ist von der Form

\[y(t) = c_1 y_1(t) + c_2 y_2(t).\]

Dabei bezeichnen \(y_1(t)\) und \(y_2(t)\) zwei sogenannte Fundamentallösungen. Die allgemeine Lösung ist also eine Linearkombination von zwei Fundamentallösungen. Diese sind Lösungen der DGL und erfüllen die Eigenschaft

\[\det\begin{pmatrix} y_1 (t) & y_2 (t) \\ \dot{y_1}(t) & \dot{y_2}(t) \end{pmatrix} \neq 0.\]

Jedes Anfangswertproblem läßt sich aufgrund dieser Eigenschaft eindeutig lösen.

Der Lösungsansatz \(e^{\lambda t}\) (Exponentialansatz) führt zur charakteristischen Gleichung \(\left(\ddot{y}(t)=\lambda^2 \cdot e^{\lambda t},~\dot{y}(t)=\lambda \cdot e^{\lambda t}\right)\)

\[\lambda^2 + a \lambda + b = 0\]

Es existieren drei Fundamentallösungen der charakteristischen Gleichung, die auf drei verschiedene Lösungen der Differentialgleichung führen:

• Fall 1: \(\lambda_1\) und \(\lambda_2\) ungleich und reell: \(y(t)=C_1 \cdot e^{\lambda_1 t}+C_2 \cdot e^{\lambda_2 t}\)

• Fall 2: \(\lambda_1=\lambda_2=:\lambda\) und reell: \(y(t)=C_1 \cdot e^{\lambda t}+C_2 \cdot t \cdot e^{\lambda t}\)

• Fall 3: \(\lambda_{1,2} = \beta\pm i\omega\): \(y(t)=e^{\beta t} \cdot [C_1 \cdot \cos(\omega t)+C_2 \cdot \sin(\omega t)]\)

Inhomogen mit konstanten Koeffizienten:

Die allgemeine Lösung der inhomogenen linearen DGL 2-ter Ordnung mit konstanten Koeffizienten

\[\ddot{y}(t) + a \dot{y}(t) + by(t) = g(t)\]

ist von der Form

\[y(t) = y_h(t) + y_p(t).\]

Dabei ist \(y_h(t)\) die allgemeine Lösung der zugehörigen homogenen DGL \(\ddot{y}(t) + a \dot{y}(t) + by(t) = 0\) und \(y_p(t)\) eine partikuläre Lösung der inhomogenen DGL. Für letztere gibt es unterschiedliche Ansätze je nach der Form von \(g(t)\), siehe Literatur.

Um eine inhomogene DGL 2. Ordnung mit konstanten Koeffizienten zu lösen, löst man folglich zuerst den homogenen Teil der Differentialgleichung. Anschließend findet man einen passenden Ansatz für die partikuläre Lösung der DGL.

Beispiel: Wir betrachten die DGL \(y''(x) - 2y'(x) + y(x) = 5 e^{-4x}\).

Die homogene DGL 2. Ordnung mit konstanten Koeffizienten lautet somit

\[y''(x) - 2y'(x) + y(x) = 0\]

und führt auf die charakteristische Gleichung

\[\lambda^2-2 \lambda +1 = 0\]

Die charakteristische Gleichung besitzt die reellwertige Doppellösung \(\lambda_1=\lambda_2=1\). Somit lautet die allgemeine homogene Lösung der DGL

\[y_h(x)=C_1\cdot e^{-x}+C_2\cdot x\cdot e^{-x}\]

Als Lösungsansatz für die partikuläre Lösung der DGL wählen wir \(y_p(x)=C\cdot e^{-4x}\). Somit ergeben sich

\[y'_p(x)=-4C\cdot e^{-4x}\] \[y''_p(x)=16C\cdot e^{-4x}\]

Eingesetzt in die ursprüngliche Differentialgleichung erhalten wir

\[16C\cdot e^{-4x}+8C \cdot e^{-4x} +C \cdot e^{-4x} = 5 \cdot e^{-4x}\]

und damit

\[C=\frac{1}{5}\]

Die allgemeine Lösung der inhomogenen Differentialgleichung ergibt sich somit als Summe der homogenen Lösung und der partikulären Lösung zu

\[y(x)=y_h(x)+y_p(x)=C_1\cdot e^{-x}+C_2\cdot x\cdot e^{-x}+\frac{1}{5}\cdot e^{-4x}\]

Eine spezifische Lösung ergibt sich über Anfangsbedingungen. Wir wählen als Anfangsbedingungen \(y(0)=6/5\) und \(y'(0)=-4/5\). Somit ergeben sich die Konstanten zu

\[C_1=1\] \[C_2=1\]

Die spezifische Lösung der DGL lautet dann

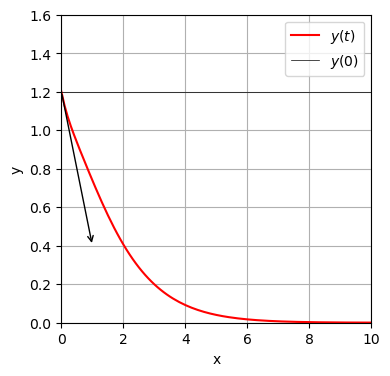
\[y(x)=y_h(x)+y_p(x)=1\cdot e^{-x}+1\cdot x\cdot e^{-x}+\frac{1}{5}\cdot e^{-4x}\]

und ist nachfolgend geplottet.

Code

x=np.arange(0,20,.1)
y=np. exp(-x)+x*np.exp(-x)+1/5*np.exp(-4*x)

plt.figure(figsize=(4,4))
plt.plot(x,y,color='red',label='$y(t)$')
plt.axhline(y=1.2,color='black',lw=.5,label='$y(0)$')
plt.annotate('',xytext=(0,1.2),xy=(1,0.4),arrowprops=dict(arrowstyle="->"))
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0,10)
plt.ylim(0,1.6)
plt.yticks(np.arange(0,1.61,.2))
plt.legend()
plt.grid(True)