Übung - Lineare Algebra I

Code 
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
import numpy.linalg as linalg
Code 
plt.rcParams['figure.figsize']=(4,4)

Aufgaben

Aufgabe LA1-1: lineare (Un-)Abhängigkeit

Sei \(v_1 = \begin{pmatrix}1 \\ 2 \\ 3 \end{pmatrix}, v_2 = \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}\) und \(v_3 = \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}\).

  1. Bestimmen Sie, ob die Vektoren \(v_i\) linear (un)abhängig sind.
  2. Falls möglich finden Sie eine Linearkombination \(\alpha_1, \alpha_2, \alpha_3\) nicht Null, so dass \(\alpha_1 v_1 + \alpha_2 v_2 + \alpha_3 v_3 = 0\).

Aufgabe LA1-2: Konturlinien

Betrachten Sie die lineare Funktion \(f:\mathbb{R}^2 \rightarrow \mathbb{R}: f(x) = 2x_1 - x_2\).

  1. Zeichnen Sie von Hand und mit Python die Konturlinien \(f(x) = c\) in \(\mathbb{R}^2\) für die Funktionswerte \(c = -2, 0, 2, 4\).
  2. Wie müssen Sie die Koeffizienten von \(f\) ändern, so dass die Konturlinien für die Funktionswerte -2, 0, 2, 4 näher zueinander bzw. weiter voneinander sind?

Aufgabe LA1-3: Prozessortemperatur

Wir nehmen an, daß die Temperatur \(T\) (gemessen über Raumtemperatur, beispielsweise \(T = 30\) Grad Celsius bedeutet 30 Grad Celsius über der Raumtemperatur) eines Computers mit zwei verschiedenen Prozessoren eine lineare Funktion der Leistungen \(p = (p_1, p_2)\) der zwei Prozessoren ist. Wenn beide Prozessoren im Leerlauf sind ist \(p = (2,2)\), was zu einer Temperatur \(T = 30\) Grad Celsius führt. Wenn der erste Prozessor mit voller Leistung arbeitet und die andere im Leerlauf ist, ist \(p = (8,2)\) und die Temperatur steigt auf \(T = 60\) Grad Celsius.

  1. Bestimmen Sie die Funktionsgleichung für \(T(p)\).
  2. Zeichnen Sie die Konturlinien von \(T(p)\) von Hand und mit Python.
  3. Angenommen beide Prozessoren laufen mit gleicher Leistung. Wie groß kann diese sein, wenn wir verlangen, dass die Temperatur unter 90 Grad Celsius sein muss?

Lösungen

Lösung LA1-1: lineare (Un-)Abhängigkeit

Die Vektoren \(v_i\) sind linear unabhängig, falls das lineare Gleichungssystem \(\alpha_1 v_1 + \alpha_2 v_2 + \alpha_3 v_3 = 0\) für die Koeffizienten \(\alpha_i \in \mathbb{R}\) nur die triviale Lösung \(\alpha_i = 0\) hat.

In komponenten ausgeschrieben lautet die Vektorgleichung \(\alpha_1 v_1 + \alpha_2 v_2 + \alpha_3 v_3 = 0\)

\[ \alpha_1 \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \alpha_2 \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} + \alpha_3 \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. \]

In Gleichungsform:

\[\begin{align} \alpha_1 + 4 \alpha_2 + 2 \alpha_3 & = 0 \\ 2 \alpha_1 + 5 \alpha_2 + \alpha_3 & = 0 \\ 3 \alpha_1 + 6 \alpha_2 & = 0 \end{align}\]

In Matrixform:

\[\begin{pmatrix} 1 & 4 & 2 \\ 2 & 5 & 1 \\ 3 & 6 & 0 \end{pmatrix} \begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}\]

Das lineare Gleichungssystem läßt sich z. B. mit dem Gaußschen Eliminationsverfahren lösen. Der Lösungsraum ist eindimensional und kann z. B. mit \(\alpha_3\) parametrisiert werden:

\[\begin{align} \alpha_1 & = 2 \alpha_3 \\ \alpha_2 & = - \alpha_3 \\ \alpha_3 & = \text{frei wählbar} \end{align}\]

Das lineare Gleichungssystem \(\alpha_1 v_1 + \alpha_2 v_2 + \alpha_3 v_3 = 0\) hat daher auch nicht-triviale Lösungen, z.B. mit \(\alpha_3 = -1\) gilt \(-2 v_1 + v_2 - v_3 = 0\). Daher sind die Vektoren linear abhängig.

Code 
# The command solve() can solve quadratic matrix equations Ax=b 
# only when Ax=b has a unique solution. This is the case 
# if and only if (short iff) the columns of A are linearly independent.
A = np.array([[1, 4, 2],
           [2, 5, 1],
           [3, 6, 0]])
b = np.zeros((3,1))
linalg.solve(A, b) # gives the trivial solution 
array([[ 0.],
       [ 0.],
       [-0.]])
Code 
# With the sympy package one can solve matrix equations Ax=b symbolically.
sp.init_printing() # initializes pretty-printing
a1, a2, a3 = sp.symbols('a1 a2 a3')
sp.linsolve([  a1 + 4*a2 + 2*a3, 
             2*a1 + 5*a2 +   a3,
             3*a1 + 6*a2     ], 
            (a1, a2, a3))

\(\displaystyle \left\{\left( 2 a_{3}, \ - a_{3}, \ a_{3}\right)\right\}\)

Lösung LA1-2: Konturlinien

  1. Die Kontourlinien sind gegeben durch die Geradengleichungen \(2x_1 - x_2 = c\). Siehe Code.
  2. Damit die Konturlinien für die Funktionswerte näher zueinander liegen, muss der Koeffizientenvektor \(\begin{pmatrix} 2 \\ -1 \end{pmatrix}\) mit einer Zahl größer 1 multipliziert werden. Damit die Konturlinien für die Funktionswerte weiter voneinander liegen, muss der Koeffizientenvektor mit einer positiven Zahl kleiner 1 multipliziert werden.
Code 
# x1-x2-Grid:
delta = 0.25
x1 = np.arange(-5.0, 5.0, delta)
x2 = np.arange(-5.0, 5.0, delta)
X1, X2 = np.meshgrid(x1, x2)

# Koeffizientenvektor:
c = np.array([2, -1])
# c = array([2, -1])*3 # Skalieren von c damit die Konturlinien näher zueinander liegen
# c = array([2, -1])*0.2 # Skalieren von c damit die Konturlinien weiter voneinander liegen

# y = f(x) = c^T x:
Y = c[0]*X1 + c[1]*X2

# Plot:
plt.figure()
plt.axis('equal')
plt.arrow(0, 0, c[0], c[1], head_width=0.2, fc='k')
CS = plt.contour(X1, X2, Y, levels= [-2,0,2,4], cmap='coolwarm')
plt.clabel(CS, inline=1, fmt='%1.1f')
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.grid(True)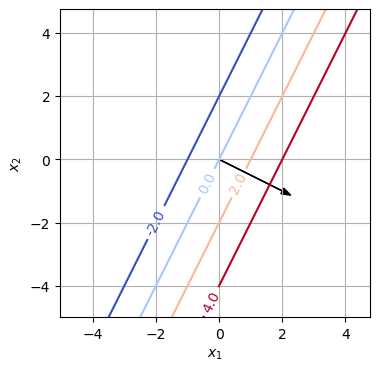

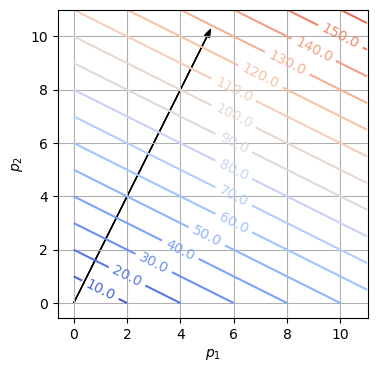
Lösung LA1-3: Prozessortemperatur

  1. Die Temperatur wird als eine lineare Funktion der Leistungen \(p = (p_1, p_2)\) modelliert: \(T(p) = c_1 p_1 + c_1 p_2\). Einsetzen der zwei Messdaten in die Funktionsgleichung liefert:

    \[\begin{align} c_1 2 + c_2 2 & = 30 \\ c_1 8 + c_2 2 & = 60 \end{align}\]

    Das lineare Gleichungssystem ist eindeutig lösbar: \(c = \begin{pmatrix} 5 \\ 10 \end{pmatrix}\), siehe auch Code. Somit lautet die Funktionsgleichung \(T(p) = 5p_1 + 10p_2\).

  2. Siehe Code.

  3. Bei gleicher Leistung \(p\) beider Prozessoren gilt \(p_1 = p_2 =p\). Die Forderung, dass die Temperatur unter 90 Grad Celsius sei, bedeutet \(5p + 10p < 90\) und hat die Lösung \(p<6\). Somit kann die gleiche Leistung beider Prozessoren maximal 6 sein, damit die Temperatur unter 90 Grad Celsius ist.

Code 
# Solving the quadratic system of linear equations in matrix form with the command solve():
A = np.array([[2, 2],
           [8, 2]])
b = np.array([[30],
           [60]])
c = linalg.solve(A, b)
print(c)
[[ 5.]
 [10.]]
Code 
# contour lines of T(p) = 5p_1 + 10p_2:

delta = 1
p1 = np.arange(0, 12, delta)
p2 = np.arange(0, 12, delta)
P1, P2 = np.meshgrid(p1, p2)

T = c[0,0]*P1 + c[1,0]*P2

plt.figure()
plt.axis('equal')
plt.arrow(0, 0, c[0,0], c[1,0], head_width=0.2, fc='k')
CS = plt.contour(P1, P2, T, levels= np.arange(0, 200, 10), cmap= 'coolwarm')  # colormaps()
plt.clabel(CS, inline=1, fmt='%1.1f')
plt.xlabel('$p_1$')
plt.ylabel('$p_2$')
plt.grid(True)