Übung - Mehrdimensionale Differentialrechnung

Code 
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
from mpl_toolkits.mplot3d.axes3d import Axes3D

Aufgaben

Aufgabe MD1: Wärmeleitungsgleichung

Zeigen Sie, dass die Temperaturfunktion \(T(x,t)= \frac{1}{\sqrt{t}}e^{-\frac{x^2}{4t}}\) die Wärmeleitungsgleichung \(\frac{\partial T}{\partial t}(x,t)= \frac{\partial^2 T}{\partial x^2}(x,t)\) erfüllt.

Aufgabe MD2: Ableitung, Differential und lineare Approximation

  1. Berechnen Sie die Jacobimatrix \(f'(x,y,z)\) der Funktion \(f:\mathbb{R}^3 \rightarrow\mathbb{R}^2: f(x, y, z)=\begin{pmatrix} \cos(x - z) \\ 4z + x y \end{pmatrix}\).
  2. Berechnen Sie das Differential der Funktion \(f:\mathbb{R}^2 \rightarrow\mathbb{R}: z(x, y) = e^{-(3x^2 + y^2)}\) allgemein und im Speziellen bei \((x_0, y_0)=(1,2)\). Wie groß ist der Unterschied zwischen der linearen Approximation der Funktionswertdifferenz \(\text{d}z\) und der wahren Funktionswertdifferenz \(\Delta z\) bei \((x_0, y_0)\), wenn \(\text{d}x = 0.1\) und \(\text{d}y = -0.2\)?

Aufgabe MD3: Partielle Ableitungen

  1. Ideales Gas: Das Volumen \(V\) einer bestimmten Menge eines idealen Gases ist durch die Temperatur \(T\) und den Druck \(p\) über die Formel \(V = 0.08\frac{T}{p}\) gegeben. Berechnen und interpretieren Sie \(\frac{\partial V}{\partial p}\) und \(\frac{\partial V}{\partial T}\) bei \(p = 20\) und \(T = 300\).
  2. Öffentlicher Personennahverkehr: In einer Vorstadt haben Pendler die Möglichkeit mit dem Bus oder mit dem Zug in das Stadtzentrum zu kommen. Die Nachfrage nach diesen Verkehrsarten variiert mit ihrer Kosten. Sei \(B(b, z)\) die Anzahl der Menschen, die mit dem Bus fahren wird, wenn \(b\) der Preis für den Bus und \(z\) der Preis der Zug sind. Zum Beispiel: Bei \(B(4, 6) = 7000\) nehmen 7000 Pendler den Bus, wenn der Preis den Bus \(4\) ist und der Preis für den Zug \(6\) ist. Erklären Sie, warum \(\frac{\partial B}{\partial b} <0\) und \(\frac{\partial B}{\partial z}> 0\) gelten.

Aufgabe MD4: Wärmeverlustfunktion - Teil 1

Ein rechteckiges Industriegebäude habe die Länge \(x\), die Breite \(y\) und die Höhe \(z\). In der Tabelle ist der Wärmeverlust pro Tag durch jede Seite des Gebäudes in geeigneten Energieeinheiten pro Quadratmeter Seitenfläche angegeben.

Dach Ostseite Westseite Nordseite Südseite Boden
10 8 6 10 5 1

Der gesamte tägliche Wärmeverlust des Gebäudes sei mit Sei \(Q(x, y, z)\) bezeichnet.

  1. Finden Sie eine Formel für \(Q(x, y, z)\).
  2. Geben Sie den gesamten täglichen Wärmeverlust an, wenn das Gebäude 30 Meter lang, 12 Meter breit und 9 Meter hoch ist.
  3. Berechnen und interpretieren Sie \(\frac{\partial Q}{\partial x} (30, 12, 9)\), \(\frac{\partial Q}{\partial y}(30, 12, 9)\) und \(\frac{\partial Q}{\partial z} (30, 12, 9)\).

Aufgabe MD5: Differential

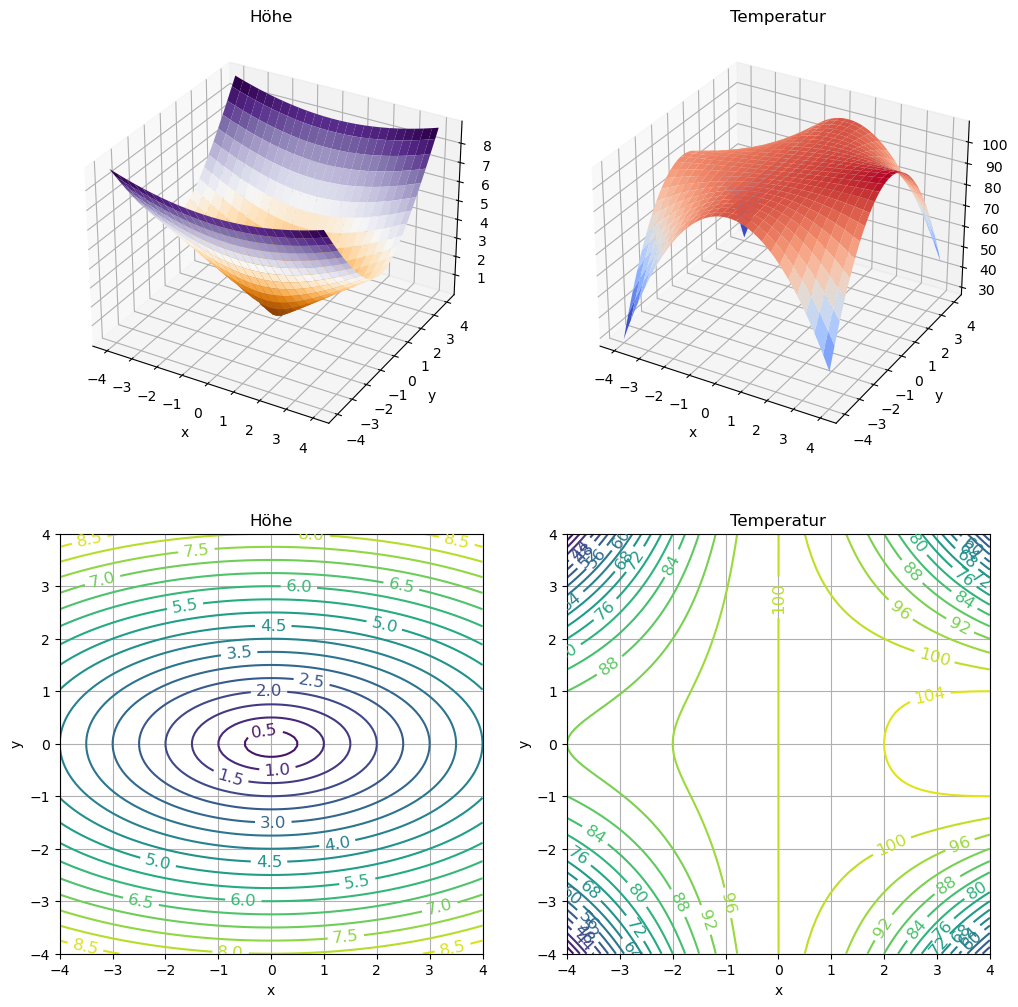
Die Höhe über Meeresspiegel eines Kraters sei gegeben durch die Funktion \(z(x,y) = \sqrt{x^2 + 4y^2}\) mit \(x, y, z\) in Kilometern. Die Temperatur in Fahrenheit sie gegeben durch \(T(x,y) = 100 + 2x -\frac{1}{4}x^2y^2\).

  1. Berechnen Sie \(\text{d}z\) und \(\text{d}T\) allgemein und speziell am Punkt \(p=(3, 2)\).
  2. Berechnen Sie die Gleichung der Tangentialebene an den Krater im Punkt \(p\).
  3. In welche Richtung steigt die Temperatur am Punkt \(p\) am stärksten an?
  4. Wie stark ändert sich am Punkt \(p\) die Temperatur pro Höhe, wenn man in die Richtung von Aufgabe 3 geht?

Lösungen

Lösung MD1: Wärmeleitungsgleichung

\(\frac{\partial T}{\partial t}(x,t)\) berechnet sich mittels Produkt- und Kettenregel zu \(e^{-\frac{x^2}{4t}}\left( -\frac{1}{2\sqrt{t^3}} + \frac{x^2}{4\sqrt{t^5}} \right)\). \(\frac{\partial T}{\partial x}(x,t)\) berechnet sich mittels Kettenregel zu \(-\frac{1}{2\sqrt{t^3}}xe^{-\frac{x^2}{4t}}\) und daraus berechnet sich \(\frac{\partial^2 T}{\partial x^2}(x,t)\) mittels Produkt- und Kettenregel zu \(e^{-\frac{x^2}{4t}}\left( -\frac{1}{2\sqrt{t^3}} + \frac{x^2}{4\sqrt{t^5}} \right)\), sodass \(\frac{\partial T}{\partial t}(x,t)= \frac{\partial^2 T}{\partial x^2}(x,t)\) erfüllt ist.

Code 
# using sympy:
sp.init_printing()
Code 
x, t = sp.symbols('x t')
T = 1/sp.sqrt(t)*sp.exp(-x**2/(4*t))
T

\(\displaystyle \frac{e^{- \frac{x^{2}}{4 t}}}{\sqrt{t}}\)

Code 
sp.simplify( sp.diff(T, t) - sp.diff(T, x, 2) )

\(\displaystyle 0\)

Code 
sp.init_printing(False)

Lösung MD2: Ableitung, Differential und lineare Approximation

  1. \(f'(x,y,z) = \begin{pmatrix} \frac{\partial}{\partial x}\cos(x - z) & \frac{\partial}{\partial y}\cos(x - z) & \frac{\partial}{\partial z} \cos(x - z) \\ \frac{\partial}{\partial x}(4z + x y) & \frac{\partial}{\partial y}(4z + x y) & \frac{\partial}{\partial z}(4z + x y) \end{pmatrix} = \begin{pmatrix}-\sin(x-z) & 0 & \sin(x-z) \\ y & x & 4 \end{pmatrix}\)

  2. \(\text{d}z = \frac{\partial z}{\partial x}\text{d}x + \frac{\partial z}{\partial y} \text{d}y = e^{-(3x^2 + y^2)}(-6x) \text{d}x + e^{-(3x^2 + y^2)}(-2y) \text{d}y\), \(\Delta z (1,2) = e^{-(3(1.1)^2 + (1.8)^2)} - e^{-(3(1)^2 + (2)^2)}\), \(\text{d}z (1,2) = e^{-7}(-6) 0.1 + e^{-7}(-4) (-0.2)\). Siehe Code:

Code 
def z(x, y):
    return np.exp(-(3*x**2 + y**2))

def dz(x_0, y_0, dx, dy): 
    return -np.exp(-(3*x_0**2 + y_0**2))*6*x_0*dx - np.exp(-(3*x_0**2 + y_0**2))*2*y_0*dy

x_0 =  1
y_0 =  2
dx  =  0.1
dy  = -0.2

print("wahre Differenz =\n {:.10f}".format( z(x_0 + dx, y_0 + dy) - z(x_0, y_0) ))
print("linear approximierte Differenz =\n {:.10f}".format( dz(x_0, y_0, dx, dy) ) )
wahre Differenz =
 0.0001265951
linear approximierte Differenz =
 0.0001823764

Lösung MD3: Partielle Ableitungen

  1. \(\frac{\partial V}{\partial p}(p,T) = -0.08\frac{T}{p^2}\) und \(\frac{\partial V}{\partial T}(p,T) = 0.08\frac{1}{p}\). Daher ist \(\frac{\partial V}{\partial p}(20, 300) = -0{,}06\) (Volumen wird kleiner bei steigendem Druck und gleichbleibender Temperatur) und \(\frac{\partial V}{\partial T}(20, 300) = 0{,}004\) (Volumen wird größer bei steigender Temperatur und gleichbleibendem Druck)
  2. \(\frac{\partial B}{\partial b} <0\) weil steigende Buspreise bei gleichbleibenden Zugpreisen zu weiniger Verwendern der Busse führen, und \(\frac{\partial B}{\partial z}> 0\) weil umgekehrt steigende Zugpreise bei gleichbleibenden Buspreisen zu mehr Verwendern der Busse führen.

Lösung MD4: Wärmeverlustfunktion - Teil 1

  1. \(Q(x,y,z) = 10xy + 8yz + 6yz + 10xz + 5xz + 1xy = 11xy + 14yz + 15xz\)
  2. \(Q(30, 12, 9)\), siehe Code
  3. Siehe Code
Code 
def Q(x,y,z):
    return 11*x*y + 14*y*z + 15*x*z

def Q_x(x,y,z):
    return 11*y + 15*z

def Q_y(x,y,z):
    return 11*x + 14*z

def Q_z(x,y,z):
    return 14*y + 15*x

x_0 = 30
y_0 = 12
z_0 =  9

print("gesamter täglicher Wärmeverlust        = {:8.2f}".format(Q(x_0, y_0, z_0)))
print("Wärmeverlust pro Meter Längenänderung  = {:8.2f}".format(Q_x(x_0, y_0, z_0)))
print("Wärmeverlust pro Meter Breitenänderung = {:8.2f}".format(Q_y(x_0, y_0, z_0)))
print("Wärmeverlust pro Meter Höhennänderung  = {:8.2f}".format(Q_z(x_0, y_0, z_0)))
gesamter täglicher Wärmeverlust        =  9522.00
Wärmeverlust pro Meter Längenänderung  =   267.00
Wärmeverlust pro Meter Breitenänderung =   456.00
Wärmeverlust pro Meter Höhennänderung  =   618.00

Lösung MD5: Differential

  1. \(\text{d}z = \frac{x}{\sqrt{x^2 + 4y^2}}\text{d}x + \frac{4y}{\sqrt{x^2 + 4y^2}}\text{d}y\), bei \(p\) gilt \(\text{d}z = 0.6\text{d}x + 1.6\text{d}y\). \(\text{d}T = (2 - 0.5xy^2)\text{d}x - 0.5x^2y\text{d}y\), bei \(p\) gilt \(\text{d}T = -4\text{d}x - 9 \text{d}y\).
  2. \(z - z(3,2) = 0.6(x - 3) + 1.6 (y - 2)\) liefert \(5z = 3x + 8y\)
  3. \(v = \text{grad}(T)(p) = (-4,-9)^T\), vgl. bei \(p\) gilt \(\text{d}T = -4\text{d}x - 9 \text{d}y\).
  4. Bei \(p\) ist \(\frac{\text{d}T(v)}{\text{d}z(v)} = \frac{-4\cdot(-4) - 9\cdot(-9)}{0.6\cdot(-4) + 1.6\cdot(-9)} = -5.77\) F/km
Code 
x = np.linspace(-4, 4, 100)
y = np.linspace(-4, 4, 100)
X, Y = np.meshgrid(x, y)

Z = np.sqrt(X**2 + 4*Y**2)
T = 100 + 2*X  - 0.25*X**2*Y**2

fig = plt.figure(figsize=(12,12),dpi=100)
ax  = fig.add_subplot(2, 2, 1, projection='3d')
p   = ax.plot_surface(X, Y, Z, rstride=4, cstride=4, linewidth=0, cmap='PuOr')
ax.view_init(azim = -60,elev = 30)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Höhe')

ax2 = fig.add_subplot(2, 2, 3)
CS = ax2.contour(X,Y,Z, 20)
ax2.clabel(CS, inline=1, fontsize=12)
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.set_title('Höhe')
ax2.grid(True)

ax3  = fig.add_subplot(2, 2, 2, projection='3d')
p   = ax3.plot_surface(X, Y, T, rstride=4, cstride=4, linewidth=0, cmap='coolwarm')
ax3.view_init(azim = -60,elev = 30)
ax3.set_xlabel('x')
ax3.set_ylabel('y')
ax3.set_title('Temperatur')

ax4 = fig.add_subplot(2, 2, 4)
CS = ax4.contour(X, Y, T, 20)
ax4.clabel(CS, inline=1, fontsize=12)
ax4.set_xlabel('x')
ax4.set_ylabel('y')
ax4.set_title('Temperatur')
ax4.grid(True)