Übung - Lineare gewöhnliche Differentialgleichungen 1. Ordnung

Code

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import sympy as sp

Code

plt.rcParams['figure.figsize']=(5,3)

Aufgaben

Aufgabe LDG1-1: Menge an \(CO_2\) in einem Raum

Die Luft in einem Raum voller Menschen enthält im Volumenanteil 0,25% Kohlendioxid (\(CO_2\)). Eine Klimaanlage wird eingeschaltet und bläst mit einer Geschwindigkeit von 500 Kubikmeter pro Minute Frischluft in den Raum. Die frische Luft vermischt sich mit der verbrauchten Luft, und das Gemisch verlässt den Raum mit einer Geschwindigkeit von 500 Kubikmeter pro Minute. Die frische Luft enthält 0,01% \(CO_2\), und der Raum hat ein Volumen von 2500 Kubikmetern.

Bestimmen Sie die DGL, die das Volumen \(y(t)\) an \(CO_2\) im Raum zu jedem Zeitpunkt \(t\) erfüllt. Lösen Sie das Anfangswertproblem, und machen Sie einen Plot der Lösung in Python.
Das in 1. entwickelte Modell ignoriert das durch die Atmung der Personen im Raum erzeugte \(CO_2\). Nehmen wir an, dass die Menschen im Raum 0,08 Kubikmeter \(CO_2\) pro Minute produzieren. Berücksichtigen Sie in einer neuen DGL diese zusätzliche \(CO_2\)-Quelle. Lösen Sie das Anfangswertproblem, und machen Sie einen Plot der Lösung in Python zum Vergleich mit der Lösung in 1..

Quelle: Goldstein, Lay et al.: Calculus & Its Applications. 13th ed., p.546, Exercise 21

Aufgabe LDG1-2: Linearer Luftwiderstand

Eine Person mit einer Masse von 70 kg springt mit einem offenen Fallschirm ohne Anfangsgeschwindigkeit aus einer Höhe von 1000 m. Die Luftwiderstandskraft sei gleich \(140v(t)\) Newton, wobei \(v(t)\) die Geschwindigkeit der Person in Metern pro Sekunde bezeichnet.

Bestimmen Sie die DGL für \(v(t)\). Lösen Sie das Anfangswertproblem und erstellen Sie einen Plot der Lösung in Python.
Bestimmen Sie die Grenzgeschwindigkeit und graphisch die Zeit bis zum Bodenkontakt.

Quelle: Bronson, Schaum’s “Differential Equations”, 3rd edition, p.60, Exercise 7.12

Aufgabe LDG1-3: RL Schaltung

Die DGL, die die elektrische Stromstärke \(I(t)\) (A) zu einem Zeitpunkt \(t\) in einer RL-Schaltung beschreibt, ist gegeben durch

\[L\dot{I} + RI = U,\]

wobei \(R\) (\(\Omega\)) den Widerstand, \(L\) (H) die Induktivität und \(U\) (V) die Spannung ist. Eine gegebene Schaltung habe eine Spannung von 5 V, einen Widerstand von 50 \(\Omega\), eine Induktivität von 1 H sowie anfangs eine Stromstärke \(I(0)=0\). Berechnen Sie die Stromstärke \(I(t)\) für \(t\geq 0\), und erzeugen Sie einen Plot der Lösung in Python.

Quelle: Bronson, Schaum’s “Differential Equations”, 3rd edition, p.52, p.65, Exercise 7.19

Aufgabe LDG1-4: Solarthermie

Das Heizungssystem eines Gebäudes bestehe aus Solarkollektoren und einem Warmwasserspeicher. Der Warmwasserspeicher habe eine Zeitkonstante von \(\frac{1}{k} = 50\) Stunden, d. h. er kühlt ohne Wärmezufuhr nach dem Newtonschen Abkühlungsgesetz \(\dot{T}(t) = - k[T(t) - T_U(t)]\) aus, wobei \(T_U(t)\) die Umgebungstemperatur zur Stunde \(t\) ist. Der solare Eintrag führt pro Stunde zu einer Temperaturerhöhung um 2 °C im Speicher. Um 9 Uhr morgens (\(t=0\)) habe der Speicher eine Wassertemperatur von 30 °C und die Umgebungstemperatur sei den ganzen Tag über bei 20 °C.

Stellen Sie die Differentialgleichung inkl. Anfangsbedingung auf, die den Temperaturverlauf des Warmwasserspeichers bei Sonneneinstrahlung ab 9 Uhr beschreibt.
Lösen Sie dieses Anfangswertproblem.

Quelle: Farlow: An Introduction to Differential Equations and Their Applications. Section 2.5, Problem 14, p. 76.

Aufgabe LDG1-5: Elektroautobatterie

Das Elektroauto Think City verfügt über eine Zebra-Batterie (Natrium-Nickelchlorid) mit einer maximalen Lade- und Entladeleistung von \(P_{\text{max}} = 30\) kW und einer Kapazität von \(E_{\text{max}} = 20\) kWh. Ein elektrischer Widerstand in der Batterie wandelt elektrische Energie in Wärme um, die die Batterie während dem Laden und Entladen auf Betriebstemperatur hält. Dieser Widerstand und folglich auch die resultierenden thermischen Verluste hängen linear vom momentanen Ladezustand der Batterie ab, bei einer Verlustleistung von minimal \(I_{\text{min}} = 40\) W und maximal \(I_{\text{max}} = 120\) W. Die in der Batterie gespeicherte Energie kann demnach für \(E(t) > 0\) beschrieben werden durch:

\[\dot{E}(t) = -I_{\text{max}} + \frac{I_{\text{max}} - I_{\text{min}}}{E_{\text{max}}} E(t) + P(t)\]

Skizzieren Sie die thermischen Verluste in Abhängigkeit der gespeicherten Energie und erklären Sie die Differentialgleichung.
Lösen Sie das Anfangswertproblem \(E(0) = 10\) kWh bei einer konstanten Ladeleistung von \(P = 20\) kW. Wann ist die Batterie vollständig geladen?
Bei einer konstanten Entladeleistung von \(P = -10\) kW, wie hoch ist der Energieinhalt der Batterie nach einer Stunde, wenn die Batterie zu Beginn voll geladen war?

Aufgabe LDG1-6: Newtonschen Abkuehlungsgesetz

Ein Körper mit einer unbekannten Temperatur wird in einen Raum mit konstanter Umgebungstemperatur von 30° C platziert. Nach 10 Minuten ist die Temperatur des Körpers 0° C und nach 20 Minuten ist sie 15° C. Bestimmen Sie die unbekannte Anfangstemperatur.

Hinweis: Newtonschen Abkühlungsgesetz \(\dot{T}(t) = - k[T(t) - T_U]\)

Quelle: Bronson: Schaum’s “Differential Equations”, Aufgabe 7.10, S. 59

Aufgabe LDG1-7: Mischung

Ein Tank enthält ursprünglich 200 Liter reines Wasser. Eine Salzlösung mit 1 kg Salz pro 4 Liter Wasser wird bei einer Rate von 12 Liter pro Minute in den Tank eingebracht. Salz und Wasser durchmischen sich perfekt, und 12 Liter der Mischung fließen pro Minute wiederum aus dem Tank heraus.

Stellen Sie die Differentialgleichung auf, die die Menge (in kg) an Salz im Tank über die Zeit hinweg beschreibt.
Lösen Sie diese Differentialgleichung.
Bestimmen Sie, falls vorhanden, den steady state.
Skizzieren Sie die Lösung.

Quelle: Farlow: Introduction to Differential Equations. Example 1, p. 61f.

Lösungen

Lösung LDG1-1: Menge an \(CO_2\) in einem Raum

\(\dot{y} = 0.05 - 0.2y, y(0) = 6.25\)
\(\dot{y} = 0.13 - 0.2y, y(0) = 6.25\)

Code

t = np.linspace(0, 60)
y0 = 0.25/100*2500
print("y0 =", y0)

if True: # numerisch
    def my_f1(y, t):
        return 0.05 - 0.2*y

    def my_f2(y, t):
        return 0.13 - 0.2*y

    y1 = odeint(my_f1, y0, t)
    y2 = odeint(my_f2, y0, t)
else: # analytisch
    y1 = 0.25 + 6.0*np.exp(-0.2*t)
    y2 = 0.65 + 5.6*np.exp(-0.2*t)

plt.figure()
plt.plot(t, y1, 'b', linewidth=2, label='ohne Menschen')
plt.plot(t, y2, 'r', linewidth=2, label='mit Menschen')
plt.ylabel('CO2 (m$^3$)')
plt.xlabel('t (Minuten)')
plt.legend()
plt.grid(True)

y0 = 6.25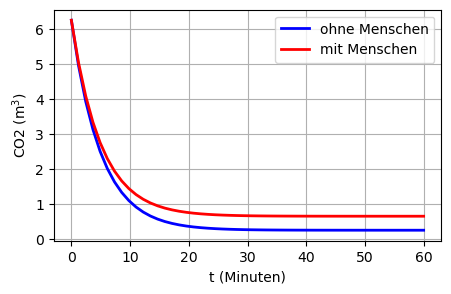

Code

sp.init_printing(use_unicode=True)
t = sp.symbols('t')
y = sp.symbols('y', cls=sp.Function)

Code

diffeq = sp.Eq(y(t).diff(t) + 0.2*y(t), 0.05)
diffeq

\(\displaystyle 0.2 y{\left(t \right)} + \frac{d}{d t} y{\left(t \right)} = 0.05\)

Code

sp.dsolve(diffeq, y(t))

\(\displaystyle y{\left(t \right)} = C_{1} e^{- 0.2 t} + 0.25\)

Code

diffeq = sp.Eq(y(t).diff(t) + 0.2*y(t), 0.13)
diffeq

\(\displaystyle 0.2 y{\left(t \right)} + \frac{d}{d t} y{\left(t \right)} = 0.13\)

Code

sp.dsolve(diffeq, y(t))

\(\displaystyle y{\left(t \right)} = C_{1} e^{- 0.2 t} + 0.65\)

Code

sp.init_printing(False)

Lösung LDG1-2: Linearer Luftwiderstand

Code

m = 70     # kg
g = 9.81   # m/s^2
r = 140    # kg/s

v_limit = -m/r*g
print(v_limit, "m/s =", v_limit*3.6, "km/h")

t = np.linspace(0, 10)
v = -m/r*g*(1 - np.exp(-r/m*t))

-4.905 m/s = -17.658 km/h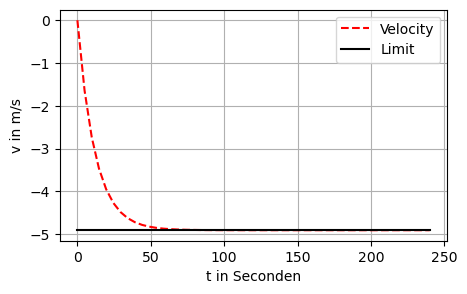

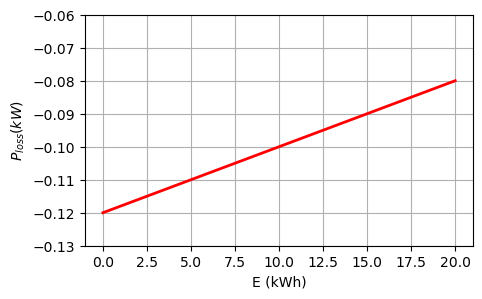
Code

plt.figure()
plt.plot(t, v,'--r',label='Velocity')
plt.plot(t, v_limit*np.ones(np.shape(t)),color='black',label='Limit')
plt.xlabel('t in Seconden')
plt.ylabel('v in m/s')
plt.legend()
plt.grid(True)

Code

t = np.linspace(0, 60*4)
#t = linspace(18, 20)

x = 1000 + (m/r)**2*g*(1 - np.exp(-r/m*t)) - m/r*g*t

plt.figure()
plt.plot(t, x,'r')
plt.xlabel('t in seconds')
plt.ylabel('x in m')
plt.grid(True)

Lösung LDG1-3: RL Schaltung

Code

t = np.linspace(0, 0.5)
I = 1/10*(1 - np.exp(-50*t))

plt.figure()
plt.plot(t, I,'r')
plt.xlabel('t')
plt.ylabel('I')
plt.grid(True)

Lösung LDG1-4: Solarthermie

\(\dot{T}(t) = - \frac{1}{50}[T(t) - 20] + 2\)
Siehe Code

Code

t = np.linspace(0,12)
T0 = 30
TU = 20
a = 1/50
b = 2 + TU*a
T = T0*np.exp(-a*t) + b/a*(1 - np.exp(-a*t))
# T = 120 - 90*exp(-t/50)

plt.figure(figsize=(5,3))
plt.plot(t + 9, T,'r')
plt.grid(True)

Lösung LDG1-5: Elektroautobatterie

Code

Emax = 20 #kWh,
Imax = 120*10**-3 #kW,
Imin = 80*10**-3 #kW
E = np.linspace(0,Emax)
Ploss = -Imax + (Imax - Imin)*E/Emax

plt.figure(figsize=(5,3))
plt.plot(E, Ploss,'r', linewidth=2)
plt.xlabel('E (kWh)')
plt.ylabel('$P_{loss} (kW)$')
plt.ylim(-Imax - 0.01, -0.06)
plt.grid(True)

Code

sp.init_printing(use_unicode=True)
Imax, Imin, Emax, P, t = sp.symbols('Imax Imin Emax P t')
E = sp.symbols('E', cls=sp.Function)

Code

diffeq = sp.Eq(E(t).diff(t), -Imax +(Imax-Imin)/Emax*E(t)+P)
diffeq

\(\displaystyle \frac{d}{d t} E{\left(t \right)} = - Imax + P + \frac{\left(Imax - Imin\right) E{\left(t \right)}}{Emax}\)

Code

sp.dsolve(diffeq, E(t))

\(\displaystyle E{\left(t \right)} = C_{1} e^{\frac{t \left(Imax - Imin\right)}{Emax}} + \frac{Emax Imax}{Imax - Imin} - \frac{Emax P}{Imax - Imin}\)

Code

sp.init_printing(False)

Umformulierung mittels \(c=e^{C_1}\):

\[E(t)=c e^{\left(\frac{I_{\text{max}} - I_{\text{min}}}{E_{\text{max}}}t\right)} + E_{\text{max}} \frac{I_{\text{max}-P}}{I_{\text{max}}-I_{\text{min}}}\]

Code

P = 20 #kW,
E0 = 10 #kWh
Emax = 20 #kWh,
Imax = 120*10** - 3 #kW,
Imin= 80*10** - 3 #kW

Code

c = E0-Emax*(Imax-P)/(Imax-Imin)
c

9950.0

Code

t = np.log((Emax - (Emax*(Imax-P)/(Imax - Imin)))/c)*Emax/(Imax - Imin)
t #min

0.5022602130027453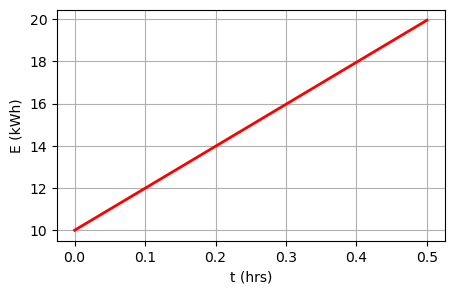

Code

t = np.linspace(0,0.5)
E = c*np.exp((Imax - Imin)/Emax*t) + Emax*(Imax - P)/(Imax - Imin)

dotE = -Imax + P + (Imax - Imin)*E/Emax
#print(dotE)

plt.figure(figsize=(5,3))
plt.plot(t, E,  '-r',  linewidth = 2)
plt.xlabel('t (hrs)')
plt.ylabel('E (kWh)')
plt.grid(True)

Code

P = -10 #kW
E0 = Emax
c = E0-Emax*(Imax-P)/(Imax-Imin)
c

-5040.0

Code

t1 =1
E  = c*np.exp((Imax-Imin)/Emax*t1)+Emax*(Imax-P)/(Imax-Imin)
E

9.90991327663869

Code

t = np.linspace(0,1.8)
E = c*np.exp((Imax-Imin)/Emax*t)+Emax*(Imax-P)/(Imax-Imin)

dotE = -Imax + P + (Imax - Imin)*E/Emax
#print(dotE)

plt.figure(figsize=(5,3))
plt.plot(t, E, '-r', linewidth=2)
plt.xlabel('t (hrs)')
plt.ylabel('E (kWh)')
plt.grid(True)

Lösung LDG1-6: Newtonschen Abkuehlungsgesetz

\(\dot{T} = -k(T - 30)\), Anfangstemperatur \(T(0)=-30\) °C

Lösung LDG1-7: Mischung

\(\dot{Q} = \frac{1}{4}12 - \frac{Q}{200}12\)
\(Q(t) = 50(1 - e^{-3t/50})\)
\(50\)
siehe Code

Code

t = np.linspace(0, 120)
Q = 50*(1 - np.exp(-3*t/50))

plt.figure(figsize=(5,3))
plt.plot(t, Q,'-r')
plt.xlabel('Zeit (Minuten)')
plt.ylabel('Menge (kg)')
plt.grid(True)