Übung - Allgemeine gewöhnliche Differentialgleichungen

Code 
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
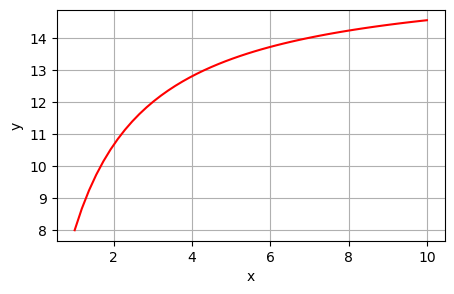
import sympy as sp
Code 
plt.rcParams['figure.figsize']=(5,3)

Aufgaben

Aufgabe ADG1: allgemeine und partikuläre Lösung

  1. Zeigen Sie, dass die Funktion \(y(x) = C\frac{x}{1 + x}\) die allgemeine Lösung der Differentialgleichung \(x(1+x)y'(x) - y(x) = 0\) ist. Wie lautet die partikuläre Lösung zum Anfangswert \(y(1)=8\)? Erstellen Sie in Python einen Plot der partikulären Lösung.

  2. Die Aufladung eines Kondensators der Kapazität \(C\) ab dem Zeitpunkt \(t=0\) über einen ohmschen Widerstand \(R\) auf die Endspannung \(u_0\) erfolgt nach dem Exponentialgesetz \(u_C(t) = u_0 (1- e^{-\frac{t}{RC}})\). Skizzieren Sie die Funktion \(u_C(t)\). Zeigen Sie, dass diese Funktion eine partikuläre Lösung der Differentialgleichung \(RC\dot{u_C}(t) + u_C(t) = u_0\) ist, die diesen Einschaltvorgang beschreibt. Erstellen Sie in Python Plots der Funktion \(u_C(t)\) für verschiedene Werte von \(C\) und \(R\).

Quellen:

  1. Papula, Band 2, Kapitel IV Gewöhnliche Differentialgleichungen, Übungsaufgaben zu Abschnitt 1, Aufgabe 1
  2. Papula, Band 2, Kapitel IV Gewöhnliche Differentialgleichungen, Übungsaufgaben zu Abschnitt 1, Aufgabe 3

Aufgabe ADG2: Trennung der Variablen

Lösen Sie folgende DGL mit der Methode der Trennung der Variablen und überprüfen Sie jeweils Ihre Ergebnisse am Computer mittels SymPy.

  1. \(y\dot{y} = te^t\)
  2. \(\dot{y}(1 + t^2) = ty\)

Quellen:

  1. Goldstein, Lay, Asmar, Schneider: Calculus & Its Applications, p.516
  2. Papula: Band 2, p.520

Aufgabe ADG3: Integration exakter DGL

Überprüfen Sie, ob die DGL exakt ist, und lösen Sie das Anfangswertproblem.

\[\dot{y} = \frac{-y^2}{2yt + 1}, \quad y(1)=-2\]

Quelle: Bronson: Schaum’s “Differential Equations”, p.36

Aufgabe ADG4: Exaktheit, allgemeine Lösung, Anfangswertproblem

Gegeben ist die Differentialgleichung \(y' = \frac{-2xy}{1 + x^2}\).

  1. Überprüfen Sie, ob die DGL exakt ist.
  2. Bestimmen Sie die allgemeine Lösung.
  3. Lösen Sie das Anfangswertproblem zur Anfangsbedingung \(y(2)=-5\).

Quelle: Bronson: Schaum’s “Differential Equations”, Aufgaben 5.2 und 5.11, S. 33 und 36

Aufgabe ADG5: Anfangswertproblem

Lösen Sie das folgende Anfangswertproblem \(yy' = \cos(2x), y(0) = -1\).

Aufgabe ADG6: Integration exakter DGL

Ist die Differentialgleichung \(\dot{y}(t) = \frac{t + \sin(y(t))}{2y(t) - t\cos(y(t))}\) exakt? Begründen Sie Ihre Antwort. Geben Sie die allgemeine Lösung der Differentialgleichung in impliziter Form an.

Aufgabe ADG7: Quadratischer Luftwiderstand

Ein Auto mit Masse \(m\) und Anfangsgeschwindigkeit \(v_0\) bewegt sich nur unter dem Einfluss des als quadratisch von der Geschwindigkeit abhängig angenommenen Luftwiderstands.

  1. Erklären Sie, warum die Geschwindigkeit \(v(t)\) des Autos die DGL \(\dot{v}(t) = -\frac{c}{m}v(t)^2\) erfüllt.
  2. Lösen Sie das Anfangswertproblem und erstellen Sie einen Plot der Lösung in Python für vernünftige Werte der Parameter.

Aufgabe ADG8: Anfangswertproblem

Lösen Sie das Anfangswertproblem

\[y' = \frac{-x}{y}, \; y(0)=1.\]

Quelle: Farlow: Introduction to Differential Equations. Example 3, p. 40f.

Lösungen

Lösung ADG1: allgemeine und partikuläre Lösung

  1. partikuläre Lösung: \(y(x) = 16\frac{x}{1 + x}\), Siehe Code.
  2. Einsetzen. Siehe Code.
Code 
x = np.linspace(1, 10)
y = 16*x/(1 + x)

plt.figure()
plt.plot(x, y,'r')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)

Code 
t = np.linspace(0, 10)
R = 1
C = 1
u0 = 1
u = u0*(1 - np.exp(-t/(R*C)))

plt.figure()
plt.plot(t, u,'r')
plt.xlabel('t')
plt.ylabel('u')
plt.grid(True)

Lösung ADG2: Trennung der Variablen

Code 
t = sp.symbols('t')
y = sp.symbols('y', cls=sp.Function)
Code 
sp.init_printing()
diffeq = sp.Eq(y(t)*y(t).diff(t), t*sp.exp(t))
diffeq

\(\displaystyle y{\left(t \right)} \frac{d}{d t} y{\left(t \right)} = t e^{t}\)

Code 
sp.dsolve(diffeq, y(t))

\(\displaystyle \left[ y{\left(t \right)} = - \sqrt{2} \sqrt{C_{1} + t e^{t} - e^{t}}, \ y{\left(t \right)} = \sqrt{2} \sqrt{C_{1} + t e^{t} - e^{t}}\right]\)

Code 
diffeq = sp.Eq(y(t).diff(t)*(1 + t**2), t*y(t))
diffeq

\(\displaystyle \left(t^{2} + 1\right) \frac{d}{d t} y{\left(t \right)} = t y{\left(t \right)}\)

Code 
sp.dsolve(diffeq, y(t))

\(\displaystyle y{\left(t \right)} = C_{1} \sqrt{t^{2} + 1}\)

Code 
sp.init_printing(False)

Lösung ADG3: Integration exakter DGL

Code 
sp.init_printing(use_unicode=True)

diffeq = sp.Eq(y(t).diff(t), -y(t)**2/(2*y(t)*t + 1))
diffeq

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = - \frac{y^{2}{\left(t \right)}}{2 t y{\left(t \right)} + 1}\)

Code 
sp.dsolve(diffeq, y(t))

\(\displaystyle \left[ y{\left(t \right)} = \frac{- \sqrt{C_{1} t + 1} - 1}{2 t}, \ y{\left(t \right)} = \frac{\sqrt{C_{1} t + 1} - 1}{2 t}\right]\)

Code 
sp.init_printing(False)

Lösung ADG4: Exaktheit, allgemeine Lösung, Anfangswertproblem

  1. ist exakt
  2. \(y= C\frac{1}{1 + x^2}\)
  3. \(y=\frac{-25}{x^2 + 1}\)

Lösung ADG5: Anfangswertproblem

\(y(x) = -\sqrt{\sin(2x) + 1}\)

Lösung ADG6: Integration exakter DGL

\(\frac{t^2}{2} + t\sin(y) - y^2 = c\)

Lösung ADG7: Quadratischer Luftwiderstand

Code 
t = np.linspace(0, 60*5) # seconds
v0 = 30               # meters per second
m = 1000              # kg
c = 1.0

v = v0/(1 + c*v0/m*t)

plt.figure()
plt.plot(t, v,'r')
plt.xlabel('t')
plt.ylabel('v')
plt.grid(True)

Lösung ADG8: Anfangswertproblem

ist exakt, \(y=\sqrt{1 - x^2}\)