Übung - Regression

Code 
import numpy as np
import matplotlib.pyplot as plt
import numpy.linalg as linalg
from scipy.optimize import linprog

Aufgaben

Aufgabe R1: Polynomiale Regression

Laden Sie mit folgenden Python-Befehlen die Daten der Datei Polyfit.csv in ein array D, dessen Spalten als Daten-Vektoren \(t\) und \(y\) weiterverwendet werden:

D = genfromtxt('Polyfit.csv', delimiter=';')
t = D[:,0]
y = D[:,1]
  1. Plotten Sie \(y\) gegen \(t\).
  2. Verwenden Sie die Methode der kleinsten Fehlerquadrate (Regression, Python-Befehl lstsq), um ein Polynom vom Grad 4 durch die Punktwolke zu fitten. Erzeugen Sie ein Stamm-Blatt-Diagramm der Koeffizienten. Warum sind die ungeraden Koeffizienten null?
  3. Plotten Sie die ursprünglichen Datenpunkte und den polynomialen Fit in eine Grafik.
  4. Benutzen Sie die Befehle polyfit und poly1d um die gleichen Resultate zu erzielen.

Aufgabe R2: Mooresches Gesetz

Mehr Information zum Beispiel unter https://de.wikipedia.org/wiki/Mooresches_Gesetz.

  1. Die Datei Moores_Law.csv enthält die Anzahlen \(n\) der Transistoren in 13 Mikroprozessoren und die Jahre derer Einführung \(t\) als Spalten. Laden Sie die Datein mit den folgenden Python-Befehlen
D = genfromtxt('Moores_Law.csv', delimiter=';')
t = D[:,0]
n = D[:,1]

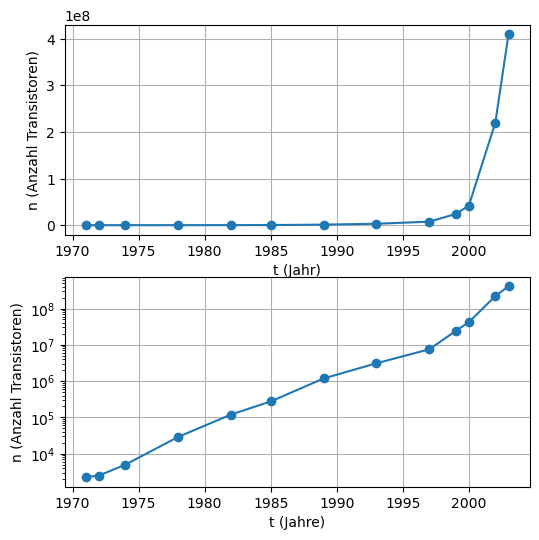
und plotten Sie \(n\) gegen \(t\) mit den Befehlen plot und semilogy. 2. Erklären Sie, wie die Methode der kleinsten Fehlerquadrate (Reggression) verwendet werden kann, um \(\alpha\) und \(t_0\) zu bestimmen, so dass

\[n_i \approx \alpha^{t_i -t_0} \text{ for } i= 1, . . . , 13\]

gilt. 3. Lösen Sie das Least-Squares-Problem (d.h. die Reggressionsaufgabe) in Python mit dem Befehl lstsq. Vergleichen Sie Ihre Resultate mit dem Mooreschen Gesetz, das behauptet, dass sich die Anzahl der Transistoren in Mikroprozessoren alle 2 Jahre verdoppelt.

Aufgabe R3: Muellmengen

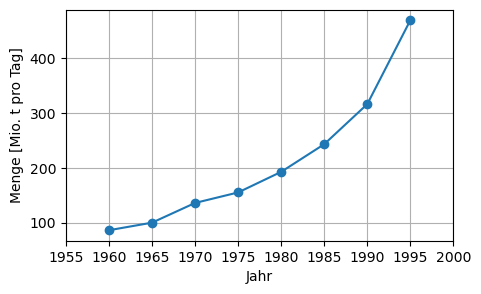
Die Müllmenge in Millionen Tonnen pro Tag des Landes Lower Slobbovia von 1960 bis 1995 ist in folgender Tabelle wiedergegeben.

Jahr \(t\) 1960 1965 1970 1975 1980 1985 1990 1995
Menge \(y\) 86.0 99.8 135.8 155.0 192.6 243.1 316.3 469.5
  1. Formulieren Sie das OLS-Problem in Matrixform für den besten Fit einer Gerade durch die Datenpunkte.
  2. Formulieren Sie das OLS-Problem in Matrixform für den besten Fit eines exponentiellen Wachstumsmodells \(y=ce^{\alpha t}\) durch die Datenpunkte.
  3. Plotten Sie die Daten, und begründen Sie, welches Modell (linear oder exponentiell) besser geeignet ist.
  4. Lösen Sie beide OLS-Problem und stellen Sie die Ergebnisse grafisch dar.

Aufgabe R4: Globale Erwärmung

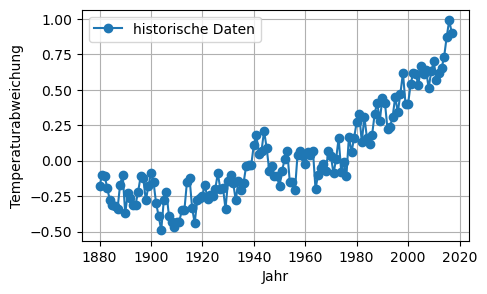
Laden Sie die Datei Global_Temperatures.csv in Python mit dem Befehl:

D = genfromtxt('Global_Temperatures.csv', delimiter=';')

Die Werte stammen von der NASA-Homepage GISS Surface Temperature Analysis. Sie repräsentieren jährliche Mittel der Abweichungen der Oberflächentemperaturen vom Mittel der Jahre 1951 bis 1980. Die erste Spalte enthält die Jahre, die zweite die jährlichen Mittelwerte, die dritte die 5-jährlichen Mittelwerte.

  1. Fitten Sie mittels der Methode der kleinsten Fehlerquadrate (Reggression) mindestens zwei sinnvolle Funktionen durch die jährlichen Mittelwerte. Stellen Sie Ihre Ergebnisse auch grafisch dar.
  2. Benutzen Sie Ihre mindestens zwei Modelle, um die jährliche mittlere Temperaturabweichung für die nächsten 30 Jahre vorherzusagen. Stellen Sie Ihre Ergebnisse auch grafisch dar.

Lösungen

Lösung R1: Polynomiale Regression

Laden der Daten, Berechnung und Darstellung der Regressionskoeffizienten:

Code 
D = np.genfromtxt('daten/Polyfit.csv', delimiter=';')
t = D[:,0]
y = D[:,1]
n = len(t)

A = np.column_stack( (np.ones((n, 1)), t, t**2, t**3, t**4) )
x = linalg.lstsq(A, y, rcond=None)[0]

for k in range(len(x)):
    print("Koeffizient der Ordnung {:d} = {:10.6f}".format(k, x[k]))

plt.figure(figsize=(5,3))
plt.stem(x)
plt.xlabel('x')
plt.xlim(-1, 5)
plt.grid(True)
Koeffizient der Ordnung 0 =   0.661640
Koeffizient der Ordnung 1 =  -0.000000
Koeffizient der Ordnung 2 =  -0.087919
Koeffizient der Ordnung 3 =   0.000000
Koeffizient der Ordnung 4 =   0.002735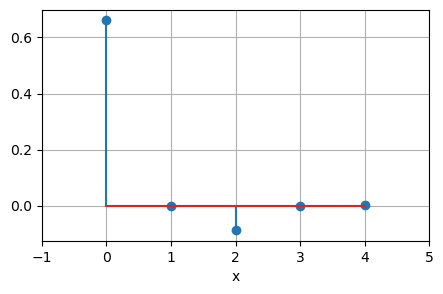

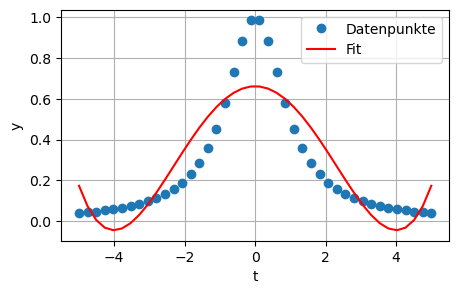
Plot des polynomialen Fits:

Code 
y_fit = A@x

plt.figure(figsize=(5,3))
plt.plot(t, y, 'o', label='Datenpunkte')
plt.plot(t, y_fit, '-r', label='Fit')
plt.xlabel('t')
plt.ylabel('y')
plt.legend(numpoints = 1)
plt.grid(True)

Befehle polyfit und poly1d:

Code 
ordnung = 4
c = np.polyfit(t, y, ordnung)

for k in range(ordnung + 1):
    print("Koeffizient der Ordnung {:d} = {:10.6f}".format(ordnung - k, c[k]))

plt.figure(figsize=(5,3))
plt.plot(t, y, 'o',label='Datenpunkte')
plt.plot(t, np.poly1d(c)(t),'-r',label='Fit')
plt.xlabel('t')
plt.ylabel('y')
plt.legend()
plt.grid(True)
Koeffizient der Ordnung 4 =   0.002735
Koeffizient der Ordnung 3 =   0.000000
Koeffizient der Ordnung 2 =  -0.087919
Koeffizient der Ordnung 1 =  -0.000000
Koeffizient der Ordnung 0 =   0.661640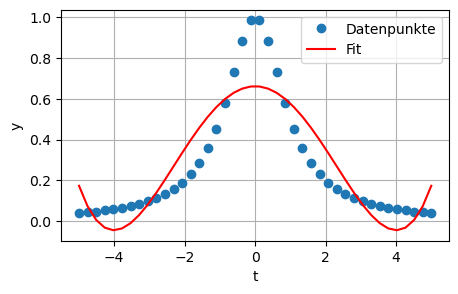

Lösung R2: Mooresches Gesetz

Code 
D = np.genfromtxt('daten/Moores_Law.csv', delimiter=';')
t = D[:,0]
n = D[:,1]
Code 
plt.figure(figsize=(6,6))

plt.subplot(211)
plt.plot(t, n, 'o-')
plt.xlabel("t (Jahr)")
plt.ylabel("n (Anzahl Transistoren)")
plt.grid(True)

plt.subplot(212)
plt.semilogy(t,n,'o-')
plt.xlabel("t (Jahre)")
plt.ylabel("n (Anzahl Transistoren)")
plt.grid(True)

\[\begin{align} n_i & = \alpha^{(t_i - t_0)} | \log() \\ \log(n_i) & = (t_i - t_0)\log(\alpha) \\ \log(n_i) & = -t_0\log(\alpha) + \log(\alpha)t_i \end{align}\]

Code 
b = np.log(n)
m = len(b)
A = np.column_stack((np.ones((m, 1)), t))
x = linalg.lstsq(A, b, rcond=None)[0]

alpha = np.exp(x[1])
t0 = -x[0]/x[1]
n_fit= alpha**(t - t0)

print("t0 = ", t0)
print("alpha^2 = ", alpha**2)
t0 =  1949.7063396217347
alpha^2 =  2.0325271695788167
Code 
plt.figure(figsize=(5,3))
plt.semilogy(t, n, 'o')
plt.semilogy(t, n_fit, '-');
plt.xlabel("t (Jahr)")
plt.ylabel("n (Anzahl Transistoren)")
plt.grid(True)

Lösung R3: Muellmengen

  1. Minimiere \(\sum_{t=1960}^{1995} (y_t - (kt + d))^2\) in Matrixform:

    \[\text{min. }\lVert\begin{pmatrix} 1960 & 1 \\ 1965 & 1 \\ \vdots & \vdots \\ 1995 & 1 \end{pmatrix} \begin{pmatrix} k \\ d \end{pmatrix} - \begin{pmatrix} 86.0 \\ 99.8 \\ \vdots \\ 469.5 \end{pmatrix} \rVert\]

  2. Logarithmieren von \(y=ce^{\alpha t}\) liefert \(\ln(y) = \alpha t + \ln(c)\).

    \[\text{min. }\lVert\begin{pmatrix} 1960 & 1 \\ 1965 & 1 \\ \vdots & \vdots \\ 1995 & 1 \end{pmatrix} \begin{pmatrix} \alpha \\ \ln(c) \end{pmatrix} - \begin{pmatrix} \ln(86.0) \\ \ln(99.8) \\ \vdots \\ \ln(469.5) \end{pmatrix} \rVert\]

  3. Siehe Code -> exponentielles Modell

Code 
t = np.arange(1960, 2000, 5)
y = np.array([86.0, 99.8, 135.8, 155.0, 192.6, 243.1, 316.3, 469.5])

plt.figure(figsize=(5,3))
plt.plot(t, y, 'o-')
plt.xlim(1955, 2000)
plt.xlabel('Jahr')
plt.ylabel('Menge [Mio. t pro Tag]')
plt.grid(True)

Code 
# linear, d. h. Gerade:
n = len(t) 
A = np.column_stack( (np.ones((n,1)),t) )
x_linear = linalg.lstsq(A, y, rcond=None)[0]
y_fit_linear = np.dot(A, x_linear)

# exponentiell:
A = np.column_stack( (np.ones((n,1)),t) )
x_exp = linalg.lstsq(A, np.log(y), rcond=None)[0]
y_fit_exp = np.exp(np.dot(A, x_exp))

plt.figure(figsize=(5, 3))
plt.plot(t, y, 'o-', label='historische Daten')
plt.plot(t, y_fit_linear, '.-r', label='linearer Fit')
plt.plot(t, y_fit_exp   , '.-g', label='exponentieller Fit')
plt.xlabel('Jahr')
plt.ylabel('Temperaturabweichung')
plt.legend(loc='best', numpoints=1)
plt.grid(True)

Lösung R4: Globale Erwärmung

Code 
D = np.genfromtxt('daten/Global_Temperatures.csv', delimiter=';')
t = D[:,0]
T = D[:,1]
n = len(t)
Code 
plt.figure(figsize=(5,3))
plt.plot(t, T, 'o-', label='historische Daten')
plt.xlabel('Jahr')
plt.ylabel('Temperaturabweichung')
plt.legend(numpoints=1, loc='best')
plt.grid(True)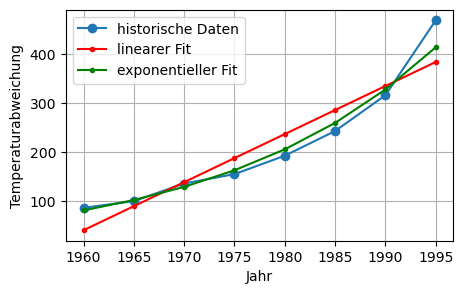

Linearer (Gerade) und quadratischer Fit via Least-Squares:

Code 
# linear, d. h. Gerade:

A = np.column_stack( (np.ones((n,1)),t) )
x_linear = linalg.lstsq(A, T, rcond=None)[0]
y_fit_linear = A@x_linear

# quadratisch:
A = np.column_stack( (np.ones((n,1)),t,t**2) )
x_quadr = linalg.lstsq(A, T, rcond=None)[0]
y_fit_quadr = A@x_quadr

plt.figure(figsize=(5,3))
plt.plot(t, T, 'o-', label='historische Daten')
plt.plot(t, y_fit_linear, '-r', label='linearer Fit')
plt.plot(t, y_fit_quadr , '-g', label='quadratischer Fit')
plt.xlabel('Jahr')
plt.ylabel('Temperaturabweichung')
plt.legend(loc='best', numpoints=1)
plt.grid(True)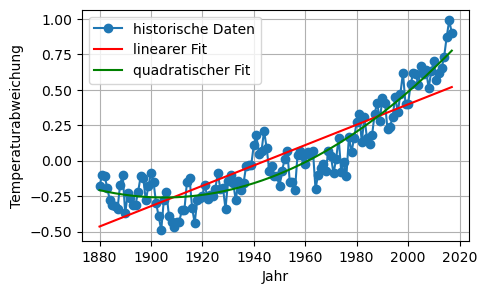

Prognosen:

Code 
t_ = np.arange(2018, 2047)
n_ = len(t_)

# linear:
A_ = np.column_stack( (np.ones((n_,1)),t_) )
y_prog_linear = A_ @ x_linear

# quadratisch:
A_ = np.column_stack( (np.ones((n_,1)),t_,t_**2) )
y_prog_quadr = A_ @ x_quadr

plt.figure(figsize=(5,3))
plt.plot(t, T, 'o-', label='historische Daten')
plt.plot(t_, y_prog_linear, '-r', label='linear')
plt.plot(t_, y_prog_quadr , '-g', label='quadratisch')
plt.xlabel('Jahr')
plt.ylabel('Temperaturabweichung')
plt.legend(numpoints=1, loc = 'best')
plt.grid(True)