Methoden

Motivation

In der Technik werden Differentialgleichungen (DGL) typischerweise verwendet, um die Dynamik eines Systems zu beschreiben. Die Lösungsmenge der DGL umfasst dann genau die möglichen zeitlichen Entwicklungen des Systems. Kennt man den Zustand des Systems zu einem Zeitpunkt und seine DGL, dann kann man alle seine zukünftigen und vergangenen Zustände berechnen. Diese sehr effiziente und erfolgreiche Vorgehensweise ist in der Physik und somit in der Technik allgegenwärtig, z. B.:

  • Die klassische Mechanik fundiert auf der Newtonschen Bewegungsgleichung, ein System von gewöhnlichen DGL 2. Ordnung.
  • Die Elektrotechnik beruht auf den Maxwell-Gleichungen, ein System von linearen partiellen DGL 1. Ordnung.
  • In der Quantenmechanik wird die Dynamik eines isolierten Systems durch die Schrödingergleichung, eine lineare partielle DGL. 1. Ordnung, bestimmt.
  • Die Navier-Stokes-Gleichungen, ein System von nichtlinearen partiellen DGL 2. Ordnung, sind zentral für die Strömungslehre.
  • Die Wärmeleitungsgleichung ist eine linear partielle DGL 2. Ordnung.

Grundbegriffe

Eine Gleichung, in der Ableitungen einer unbekannten Funktion, z. B. \(y(x)\), bis zur \(n\)-ten Ordnung auftreten, heißt eine gewöhnliche DGL \(n\)-ter Ordnung. Analog heißt eine Gleichung für eine Funktion von mehr als einer Variablen, z. B. \(u(x,y,z)\), die partielle Ableitungen enthält, partielle DGL. Da wir uns in dieser Lehrveranstaltung nur mit gewöhnlichen DGL beschäftigen werden, verwenden wir als Abkürzung der Einfachheit halber nur DGL.

Eine Funktion \(y(x)\) heißt Lösung oder Integralkurve einer DGL, wenn sie die DGL für alle \(x\) des Definitionsbereichs der Funktion erfüllt. Die allgemeine Lösung einer DGL \(n\)-ter Ordnung enthält \(n\) unabhängige, frei wählbare Parameter, die Integrationskonstanten genannt werden. Eine spezielle (=partikuläre) Lösung der DGL kann aus der allgemeinen Lösung gewonnen werden, indem aufgrund zusätzlicher Bedingungen, z. B. Anfangs- oder Randbedingungen, die Werte der \(n\) Integrationskonstanten fixiert werden. Wenn neben der DGL auch ausreichend viele Anfangsbedingungen gegeben sind, heißt die Suche nach der zugehörigen partikulären Lösung Anfangswertproblem.

Beispiele:

  • Die DGL \(y'(x) = 2x\) lässt sich durch unbestimmte Integration lösen. Ihre allgemeine Lösung lautet \(y(x) = x^2 + C\) mit Integrationskonstante \(C \in \mathbb{R}\).
  • Die DGL \(y'(x) = \lambda y(x)\) beschreibt für negatives \(\lambda\) z. B. radioaktiven Zerfall und für positives \(\lambda\) exponentielles Wachstum. Die allgemeine Lösung lautet \(y(x) = Ce^{\lambda x}\) mit der Integrationskonstante \(C \in \mathbb{R}\).
  • Die 1-dimensionalen Bewegungen \(x(t) = s_0 + v_0 t + \frac{1}{2}gt^2\) bilden die allgemeine Lösung der Bewegungsgleichung \(m \ddot{x}(t) = F\) für eine konstante Kraft \(F\) und somit für eine konstante Beschleunigung \(g = \frac{F}{m}\) einer Masse \(m\). Der Anfangsort \(x_0\) und die Anfangsgeschwindigkeit \(v_0\) sind die Integrationskonstanten.
  • Die harmonischen Schwingungen \(x(t) = A\sin(\omega_0 t + \varphi)\) bilden die allgemeine Lösung der DGL \(\ddot{x}(t) + \omega_0^2 x(t) = 0\). Die Amplitude \(A\) und die Phase \(\varphi\) sind die Integrationskonstanten.

Oft schreibt man eine DGL, z. B. \(y'(x) = -\lambda y(x)\), ohne Argument \(x\), also \(y' = -\lambda y\).

DGL 1. Ordnung

Wir betrachten DGL 1. Ordnung von der Form \[ y'(x) = f(x, y(x)). \] Dabei ist \(f\) eine vorgegebene Funktion, die die Steigung \(y'(x)\) der gesuchten Funktion \(y(x)\) an jedem Punkt \((x, y(x))\) ihres Graphen in der \(x\)-\(y\)-Ebene angibt.

Beispiele: \(y'(x) = 2x\), \(y'(x) = -\lambda y(x)\), \(y'(x) = -\frac{x}{y(x)}\).

An jedem Punkt \((x, y)\) der \(x\)-\(y\)-Ebene wird also durch \(f(x, y)\) eine Steigung (Richtung) vorgeschrieben, die von einer Lösung \(y(x)\) erfüllt werden muss, wenn sie durch diesen Punkt geht. Die Funktion \(f(x, y)\) wird als Richtungsfeld der DGL bezeichnet.

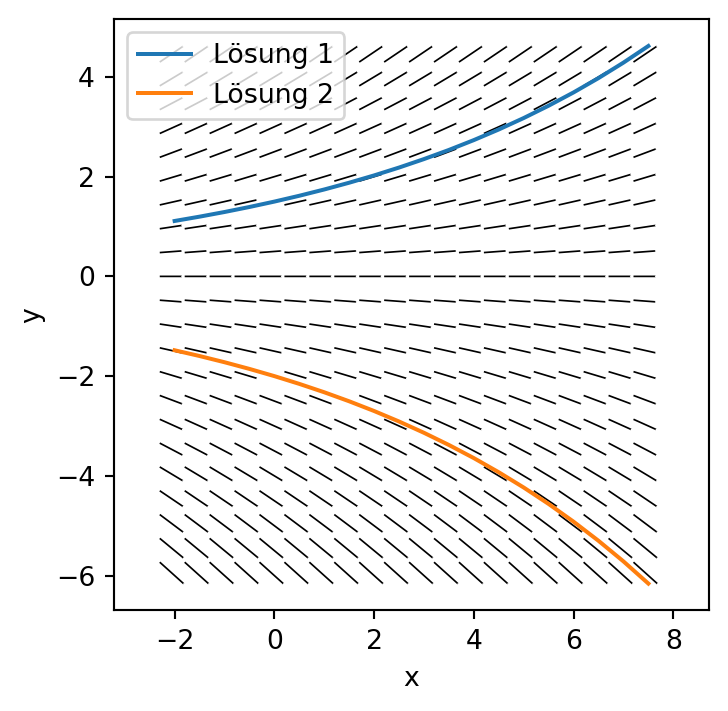
Beispiel (exponentielles Wachstum): Für eine Wachstumskonstante \(\lambda \geq 0\) betrachten wir die DGL \(y' = \lambda y\). Das Richtungsfeld \(f(x, y) = \lambda y\) hängt nur von \(y\) ab. Die Integralkurven sind \(y(x)= Ce^{\lambda x}\). Die Integrationskonstante \(C\) ist gleich dem Anfangswert \(y(0)\). In Abbildung 1 ist das Richtungsfeld und zwei Lösungen für \(\lambda = 0{,}15\) dargestellt.

Abbildung 1: Exponentiellen Wachstum: Richtungsfeld und zwei Lösungen

Trennung der Variablen

DGL 1. Ordnung, die die Form \(y'(x) = f(x) \cdot g(y)\) haben, heißen separabel und lassen sich mittels der Methode “Trennung der Variablen” in folgenden Schritten lösen:

  1. Schreibe \(\frac{\text{d}y}{\text{d}x} = f(x) \cdot g(y)\).
  2. Trenne die Variablen: \(\frac{\text{d}y}{g(y)} = f(x) \,\text{d}x\).
  3. Integriere beide Seiten: \(\int \frac{\text{d}y}{g(y)} = \int f(x) \,\text{d}x\).
  4. Löse die resultierende Gleichung falls möglich nach \(y\) auf.

Beispiel: Wir lösen die separable DGL \(y' + y^2 = 0\). \[ \begin{aligned} y' & = -y^2 \\ \frac{\text{d}y}{\text{d}x} &= -y^2 \\ -\frac{1}{y^2}\,\text{d}y &= \text{d}x \\ \int -\frac{1}{y^2}\,\text{d}y &= \int\text{d}x \\ - \frac{y^{-1}}{-1} &= x + C \\ \frac{1}{y} &= x + C \\ y(x) &= \frac{1}{x + C} \end{aligned} \]

Substitutionen

DGL der Form \(y' = f(ax + by + c)\) mit \(a, b \neq 0, c \in \mathbb{R}\) werden durch die Substitution \(u(x) := ax + by(x) + c\) in eine separable DGL für die Funktion \(u(x)\) transformiert. Genauer: Durch Ableiten der Substitution \(u = ax + by + c\) erhalten wir \(u' = a + by'\), was durch Umformen \(y' = \frac{u' - a}{b}\) ergibt. Damit können wir die ursprüngliche DGL transformieren und trennen: \[ \begin{aligned} y' & = f(ax + by + c) \\ \frac{u' - a}{b} & = f(u) \\ u ' &= a + b f(u) \\ \frac{\text{d}u}{\text{d}x} &= a + b f(u) \\ \frac{1}{a + b f(u)} \,\text{d}u &= \text{d}x \end{aligned} \] Die DGL für \(u(x)\) lässt sich also durch Trennen der Variablen lösen. Anschließend erhält man durch Rücksubstitution die Lösung für \(y(x)\).

Analog werden DGL der Form \(y' = f\left( \frac{y}{x} \right)\) durch die Substitution \(u(x) := \frac{y(x)}{x}\) in eine separable DGL für die Funktion \(u(x)\) transformiert. Genauer: Wir schreiben die Substitution als \(y(x) = x\cdot u(x)\). Ableiten dieser Gleichung liefert \(y' = 1 \cdot u + x \cdot u'\). Damit können wir die ursprüngliche DGL transformieren und trennen: \[ \begin{aligned} y' & = f\left( \frac{y}{x} \right) \\ u + x \cdot u' &= f(u) \\ u + x \cdot \frac{\text{d}u}{\text{d}x} &= f(u) \\ \frac{1}{f(u) - u}\,\text{d}u &= \frac{\text{d}x}{x} \end{aligned} \] Die DGL für \(u(x)\) lässt sich also durch Trennen der Variablen lösen. Anschließend erhält man durch Rücksubstitution die Lösung für \(y(x)\).

Lineare DGL 1. Ordnung

Achtung

Ab jetzt schreiben wir die zu suchende Funktion als \(y(t)\) und ihre Ableitungen als \(\dot{y}(t)\). Das machen wir, weil in sehr vielen Anwendungen die unabhängige Variable die Zeit \(t\) ist. Zudem ist es eine gute Übung, um sich freier von Bezeichnungen zu machen.

Eine DGL 1. Ordnung heißt linear, wenn sie in der Form \[ \dot{y}(t) + f(t) \cdot y(t) = g(t) \] darstellbar ist. Ist \(g(t) = 0\) für alle \(t\), so heißt die lineare DGL homogen, ansonsten inhomogen. Für homogene, lineare DGL gilt die Superpositionsregel: Sind \(y_1(t)\) und \(y_2(t)\) Lösungen der DGL, dann ist auch jede Linearkombination \(y(t) = c_1 y_1(t) + c_2 y_2(t)\) mit \(c_1, c_2 \in \mathbb{R}\) eine Lösung.

Beispiele:

  • \(\dot{y}(t) - t \cdot y(t) = 0\) ist linear und homogen.
  • \(t \cdot \dot{y}(t) + 2 y(t) = e^t\) ist linear und inhomogen.
  • \(\dot{y}(t) +\tan(t) \cdot y(t) = 2\sin(t)\cos(t)\) ist linear und inhomogen.
  • \(\dot{y}(t) + y^2(t) = 1\) ist nicht linear.
  • \(y(t) \cdot \dot{y}(t) + t = 0\) ist nicht linear.

Eine homogene lineare DGL 1. Ordnung \(\dot{y}(t) + f(t) \cdot y(t) = 0\) kann durch Trennen der Variablen integriert werden. Die allgemeine Lösung lautet \[ y(t) = C e^{-\int f(t) \,\text{d}t}\;\text{mit } C\in \mathbb{R}. \] Für eine inhomogene lineare DGL 1. Ordnung \(\dot{y}(t) + f(t) \cdot y(t) = g(t)\) gibt es unter anderem folgende zwei Lösungsmethoden:

  • Aufsuchen einer partikulären Lösung: Diese Methode beruht auf der Tatsache, dass die allgemeine Lösung \(y(t)\) der inhomogenen linearen DGL als Summe der allgemeinen Lösung \(y_0(t)\) der zugehörigen homogenen linearen DGL und einer beliebigen partikulären Lösung \(y_p(t)\) der inhomogenen linearen DGL darstellbar ist: \(y(t) = y_0(t) + y_p(t)\). Dies gilt auch für lineare DGL höherer Ordnung.
  • Die Methode der “Variation der Konstanten”, siehe z. B. [1], verwendet zum Aufsuchen einer partikulären Lösung den Ansatz, die Integrationskonstante \(C\) der homogenen Lösung \(y(t) = C e^{-\int f(t) \,\text{d}t}\) als Funktion \(C(t)\) zu betrachten. Dieser Ansatz wird anschließend in die inhomogene DGL eingesetzt, um \(C(t)\) zu bestimmen. Alternativ kann man die folgende Lösungsformel verwenden: \[ y(t) = \left[ \int g(t) \cdot e^{\int f(t) \,\text{d}t} \,\text{d}t + C \right] e^{-\int f(t) \,\text{d} t} \;\text{mit } C\in \mathbb{R}. \]

Ein sehr oft auftretender Spezialfall besteht aus den linearen DGL 1. Ordnung mit konstanten Koeffizienten \[ \dot{y}(t) + ay(t) = b \text{ mit } a, b \in \mathbb{R}. \] Wir schreiben die allgemeine Lösung auf zwei alternative Arten: \[ \begin{aligned} y(t) &= \left(y(0)- \frac{b}{a}\right)e^{-at} + \frac{b}{a} \\ y(t) & = y(0)e^{-at} + \frac{b}{a}\left( 1 - e^{-at} \right) \end{aligned} \] Dabei wird die Integrationskonstante jeweils durch den Anfangszustand \(y(0)\) angegeben. Das Verhalten der Lösung ist dadurch leicht interpretierbar:

  • Falls \(a < 0\), divergiert \(y(t)\), ausser der Anfangszustand ist gleich dem steady state Wert: \(y(0)=\frac{b}{a}\). Beim steady state (=Gleichgewichtszustand) bleibt \(y(t)\) konstant, d. h. \(\dot{y}(t) = 0\).
  • Falls \(a > 0\), konvergiert \(y(t)\) vom Anfangswert \(y(0)\) zum steady state Wert \(\frac{b}{a}\). Der Anteil \(y(0)e^{-at}\) beginnt bei \(y(0)\) und geht gegen Null. Der Anteil \(\frac{b}{a}\left( 1 - e^{-at} \right)\) beginnt bei Null und geht gegen \(\frac{b}{a}\).

DGL 2. Ordnung

Wir beschränken uns auf lineare DGL 2. Ordnung mit konstanten Koeffizienten. Diese haben die Form \[ \ddot{y}(t) + a\dot{y}(t) + by(t) = g(t) \] mit \(a, b \in \mathbb{R}\) und einer evtl. zeitabhängigen Inhomogenität \(g(t)\). Falls \(g(t) = 0\) für alle \(t\), dann heißt die DGL homogen, ansonsten inhomogen. DGL von diesem Typ finden sehr viele Anwendungen in der Technik, da sie harmonische, gedämpfte, erzwungene Schwingungen modellieren, siehe z. B. Wikipedia.

Beispiele:

  • Die eindimensionale Bewegung eines Massenpunktes unter dem Einfluss einer linearen Rückstellkraft und einer Reibungskraft, die proportional zu seiner Geschwindigkeit ist: Um die zugehörige DGL zu bestimmen, verwenden wir Newtons Bewegungsgleichung und erhalten: \[ m\ddot{y}(t) = -d \dot{y}(t) - k y(t). \tag{1}\] Bezeichnungen:

    • \(m\) … Masse des Massenpunkts
    • \(y(t)\) … eindimensionaler Ort zum Zeitpunkt \(t\)
    • \(-d\dot{y}(t)\) … Reibungskraft mit positiver Konstante \(d\)
    • \(-ky(t)\) … lineare Rückstellkraft mit positiver Konstante \(k\)

  • Elektrotechnik: Der Strom \(i(t)\) als Funktion der Zeit \(t\) im RLC-Schwingkreis erfüllt die DGL \[ LC \frac{\text{d}^{2}i}{\text{d}t^{2}}(t) + RC \frac{\text{d}i}{\text{d}t}(t) + i(t) = 0, \] wobei \(\frac{\text{d}^{2}i}{\text{d}t^{2}}(t)\) die zweite Ableitung von \(i(t)\) bezeichnet.

Beispiel für Exponentialansatz

Fortsetzung des ersten Beispiels: Zur Bestimmung der Bewegung \(y(t)\) des Massenpunktes schreiben wir zuerst die Bewegungsgleichung (1) in der Form: \[ \ddot{y} + \frac{d}{m}\dot{y} + \frac{k}{m}y = 0. \] Dann untersuchen wir, ob und, falls ja, für welche Werte von \(\lambda\) der Ansatz \(y(t) = e^{\lambda t}\) die DGL löst. Einsetzen des Ansatzes in die DGL liefert \[ \begin{aligned} \lambda^2 e^{\lambda t} + \frac{d}{m} \lambda e^{\lambda t} + \frac{k}{m} e^{\lambda t} &= 0 \\ \lambda^2 + \frac{d}{m} \lambda + \frac{k}{m} &= 0 \\ \lambda_{1,2} &= -\frac{d}{2m} \pm \sqrt{\frac{d^2 - 4mk}{4m^2}} \\ \lambda_{1,2} &= -\frac{d}{2m} \pm \sqrt{-1}\frac{\sqrt{4mk - d^2}}{2m} \\ \lambda_{1,2} &= -\frac{d}{2m} \pm i \omega. \end{aligned} \] Dabei haben wir \(\omega := \frac{\sqrt{4mk - d^2}}{2m}\) gesetzt und angenommen, dass \(d^2 \leq 4mk\) gilt, d. h. dass die Dämpfung im Vergleich zur Rückstellkraft und zur Masse schwach ist. Unter dieser Annahme ist \(\omega\) reell und wird als die Kreisfrequenz der gedämpften Schwingung bezeichnet. Die Kreisfrequenz der ungedämpften Schwingung mit \(d=0\) wird mit \(\omega_0\) bezeichnet und hat den Wert \(\omega_0 = \frac{\sqrt{4mk - 0}}{2m} = \sqrt{\frac{k}{m}}.\) Wir bemerken, dass \(\omega_0 \geq\omega\) gilt, Dämpfung die Kreisfrequenz also verkleinert.

Da die DGL (1) linear und homogen ist, ist die allgemeine Lösung die Linearkombination der beiden Exponentialfunktionen \(e^{\lambda_1 t}\) und \(e^{\lambda_2 t}\): \[ y(t) = C_1 e^{\lambda_1 t} + C_2 e^{\lambda_2 t}, \] wobei die Konstanten \(C_1\) und \(C_2\) komplexe Zahlen sind. Da die DGL (1) linear und homogen ist, sind zudem sowohl der Real- als auch der Imaginärteil einer Lösung wieder Lösung. Ihre allgemeine reelle Lösung lautet daher \[ y(t) = e^{-\frac{d}{2m}t} \left[c_1 \cos(\omega t) + c_2 \sin(\omega t)\right] \] mit reellen Konstanten \(c_1\) und \(c_2\). Sie besteht aus der exponentiellen Dämpfung \(e^{-\frac{d}{2m}t}\) und der ungedämpften harmonischen Schwingung \(c_1 \cos(\omega t) + c_2 \sin(\omega t)\) mit Kreisfrequenz \(\omega\).

Allgemeine Lösungsstruktur

Homogen mit konstanten Koeffizienten: Die allgemeine Lösung der homogenen linearen DGL 2. Ordnung mit konstanten Koeffizienten \[ \ddot{y}(t) + a \dot{y}(t) + by(t) = 0 \] ist eine Linearkombination \(y(t) = c_1 y_1(t) + c_2 y_2(t)\) von zwei sogenannten Fundamentallösungen \(y_1(t)\) und \(y_2(t)\). Diese sind Lösungen der DGL und erfüllen die Eigenschaft \(y_1 (t) \cdot \dot{y_2}(t) - y_2 (t) \cdot \dot{y_1}(t) \neq 0\) für mindestens ein \(t\). Jedes Anfangswertproblem lässt sich aufgrund dieser Eigenschaft eindeutig lösen. Der Exponentialansatz \(e^{\lambda t}\) führt zur charakteristischen Gleichung \[ \lambda^2 + a \lambda + b = 0 \] mit Lösungen \(\lambda_1\) und \(\lambda_2\) und folgenden zugehörigen Fundamentallösungen:

  • \(\lambda_1\) und \(\lambda_2\) ungleich und reell: \(y_1(t)=e^{\lambda_1 t}\) und \(y_2(t)=e^{\lambda_2 t}\), für negative \(\lambda_1\) und \(\lambda_2\) heißt dieser Fall Kriechfall
  • \(\lambda_1=\lambda_2=:\lambda\) und reell: \(y_1(t)=e^{\lambda t}\) und \(y_2(t)=te^{\lambda t}\), für negatives \(\lambda\) heißt dieser Fall Aperiodischer Grenzfall
  • \(\lambda_{1,2} = \beta \pm j \omega\): \(y_1(t)=e^{\beta t}\cos(\omega t)\) und \(y_2(t)=e^{\beta t}\sin(\omega t)\), für negatives \(\beta\) heißt dieser Fall Schwingfall

Inhomogen mit konstanten Koeffizienten: Die allgemeine Lösung der inhomogenen linearen DGL 2. Ordnung mit konstanten Koeffizienten \[ \ddot{y}(t) + a \dot{y}(t) + by(t) = g(t) \] ist von der Form \[ y(t) = y_0(t) + y_p(t) \] Dabei ist \(y_0(t)\) die allgemeine Lösung der zugehörigen homogenen DGL \(\ddot{y}(t) + a \dot{y}(t) + by(t) = 0\) und \(y_p(t)\) eine partikuläre Lösung der inhomogenen DGL. Für letztere gibt es unterschiedliche Ansätze je nach der Form von \(g(t)\), siehe z. B. [1] Kapitel IV, Abschnitt 3, Seite 408f.

Beispiele

Trennung der Variablen

Wir lösen die DGL \(y'=y\), siehe auch [1] S. 359. \[ \begin{aligned} \frac{\text{d}y}{\text{d}x} &= y \\ \frac{1}{y }\text{d}y & = \text{d}x \\ \int \frac{1}{y }\text{d}y & = \int \text{d}x \\ \ln |y| &= x + C, \; C\in \mathbb{R} \\ |y| &= e^{x + C} \\ y &= \pm e^C e^x \\ y &= K e^x, \; K \neq 0 \end{aligned} \] Wir überprüfen noch, ob \(K=0\) auch eine Lösung liefert. Für \(K=0\) ist \(y=0\) und somit \(y'=0\). Einsetzen in die DGL zeigt, dass \(y=0\) auch eine Lösung ist. Insgesamt lautet die allgemeine Lösung der DGL daher \(y(x) = K e^x\) mit \(K \in \mathbb{R}\).

Dieses Beispiel ist mit dem Exponentialansatz, der für homogene lineare DGL mit konstanten Koeffizienten geeignet ist, einfacher zu lösen. Wir setzen \(y(x) = e^{\lambda x}\) und \(y'(x) = \lambda e^{\lambda x}\) in die DGL ein: \(\lambda e^{\lambda x} = e^{\lambda x}\). Division durch \(e^{\lambda x}\) liefert \(\lambda = 1\) und \(y(x) = e^x\) als Lösung. Da die DGL homogen linear ist, ist auch jedes Vielfache \(y(x) = K e^x\) mit \(K \in \mathbb{R}\) eine Lösung.

Substitution A

Wir lösen die DGL \(y' = 2x - y\), siehe auch [1] S. 364. Die DGL ist vom Typ \(y'(x) = f(ax + by + c)\) mit \(a=2\), \(b=-1\) und \(c=0\). Daher transformieren wir sie mit der Substitution \(u(x) = ax + by + c = 2x - y\). Ableiten von \(u = 2x - y\) nach \(x\) liefert \(u' = 2 - y'\). Daher ist \(y' = 2 - u'\). Einsetzen in die DGL ergibt \[ \begin{aligned} 2 - u' &= u \\ - \frac{\text{d}u}{\text{d}x} &= u -2 \\ \frac{1}{u - 2}\text{d}u &= - \text{d}x \\ \ln|u-2| &= -x + C, \; C\in \mathbb{R} \\ |u-2| &= e^C e^{-x} \\ u-2 & = \pm e^C e^{-x} \\ u &= 2 + K e^{-x}, \; K \neq 0 \end{aligned} \] Wir überprüfen noch, ob \(K=0\) auch eine Lösung liefert. Für \(K=0\) ist \(u = 2\) und \(u'=0\). Einsetzen in die DGL \(2 - u' = u\) zeigt, dass \(u=2\) auch eine Lösung ist. Die Rücksubstitution liefert die allgemeine Lösung der ursprünglichen DGL: \(y(x) = 2x - 2 - K e^{-x}\) mit \(K\in \mathbb{R}\).

Substitution B

Wir lösen die DGL \(y' = \frac{x + 2y}{x}\), siehe auch [1] S. 364. Umformen der rechten Seite ergibt \(y' = 1 + 2\frac{y}{x}\). Die DGL ist also vom Typ \(y'(x) = f\left( \frac{y}{x} \right)\). Aus der Substitution \(u = \frac{y}{x}\) folgt \(y' = 1 \cdot u + x \cdot u'\). Einsetzen in die DGL ergibt \[ \begin{aligned} u + x \cdot u' &= 1 + 2u \\ x \cdot u' &= 1 + u \\ x \frac{\text{d}u}{\text{d}x} &= 1 + u \\ \frac{1}{1+u} \text{d}u &= \frac{1}{x} \text{d}x \\ \ln|1+u| &= \ln |x| + C, \; C\in \mathbb{R} \\ 1+u = \pm e^C x \\ u = K x - 1, \; K \neq 0 \end{aligned} \] Wir überprüfen noch, ob \(K=0\) auch eine Lösung liefert. Für \(K=0\) ist \(u = -1\) und \(u'=0\). Einsetzen in die DGL \(x \cdot u' = 1 + u\) zeigt, dass \(u = -1\) auch eine Lösung ist. Die Rücksubstitution liefert die allgemeine Lösung der ursprünglichen DGL: \(y(x) = Kx^2 - x\) mit \(K\in \mathbb{R}\).

Newtons Abkühlgesetz

Wir suchen die Temperatur \(T_W(t)\) einer Tasse Glühwein als Funktion der Zeit \(t\). Der Glühwein befindet sich in einer Umgebung mit konstanter Umgebungstemperatur \(T_U\). Newtons Abkühlgesetz besagt, dass der Energieverlust pro Zeit durch Wärmeübertragung an die Umgebung, geschrieben als \(\dot{Q}(t)\), die Gleichung \[ \dot{Q}(t) = -d [T_W(t) - T_U] \] mit einer positiven Konstante \(d\) (Abkühlkoeffizient) erfüllt. Aus \(\dot{Q}(t) = cm\dot{T_W}(t)\) (\(m\) die Masse des Glühweins, \(c\) seine spezifische Wärmekapazität) folgt \[ cm\dot{T_W}(t) = -d [T_W(t) - T_U] \] als Differentialgleichung für die Temperatur \(T_W(t)\). Wir führen die Temperaturdifferenz zur Umgebung als neue abhängige Variable ein: \(T(t) := T_W(t) - T_U\), und beachten, dass \(\dot{T}(t) = \dot{T_W}(t)\) gilt. Dadurch erhalten wir die kompaktere Differentialgleichung \[ \dot{T}(t) = -\lambda T(t) \] mit dem einzigen Parameter \(\lambda=\frac{d}{cm}\), der den Zeitverlauf bestimmt.

Lösung: \(T(t) = T(0)e^{-\lambda t}\), d. h. die Temperaturdifferenz zur Umgebung klingt exponentiell vom Anfangswert \(T(0)\) ab. Je größer \(\lambda\) ist, umso schneller kühlt der Glühwein aus.

Elektrischer Schaltkreis

Der Strom \(I(t)\) als Funktion der Zeit \(t\) erfüllt in einem elektrischen Schaltkreis mit vorgegebener konstanter Spannung \(U\) und in Serie geschaltetem ohmschen Widerstand \(R\) und Induktivität \(L\) die DGL \[ L\dot{I} + RI = U. \] Nach Umformen zu \(\dot{I} + \frac{R}{L}I = \frac{U}{L}\) können wir die Lösungsformel verwenden. Die Lösung lautet \[ I(t)= I(0)e^{-\frac{R}{L}t} + \frac{U}{R}\left(1 - e^{-\frac{R}{L}t}\right). \] Der Strom konvergiert zum steady state Wert \(\frac{U}{R}\).

Verschmutztes Wasser

Ein See enthält \(4 \cdot 10^7\) Liter reines Wasser zum Zeitpunkt \(t=0\). Anschließend fließt verschmutztes Wasser in den See, das \(0{,}67\) Liter Schadstoff und 10 Liter reines Wasser pro Sekunde in den See bringt. Wir nehmen an, dass sich das eingebrachte verschmutzte Wasser sofort mit dem Seewasser vermischt. Pro Sekunde fließen \(10{,}67\) Liter aus dem See hinaus. Wir bestimmen die Menge an Schadstoff im See als Funktion der Zeit. Mit \(y(t)\) bezeichnen wir die Liter Schadstoff für Zeitpunkte \(t\geq 0\). Der Anteil an Schadstoff pro Liter Seewasser beträgt \(\frac{y(t)}{4 \cdot 10^7}\).

  • Aufstellen der DGL: Die Änderung der Schadstoffmenge im See ist gleich der Abflussmenge an Schadstoff pro Zeit plus der Einflussmenge pro Zeit, d. h. \(\dot{y} = -10{,}67\frac{y}{4 \cdot 10^7} + 0{,}67\). Die Terme der DGL haben die Einheit Liter pro Sekunde.
  • Lösung: \(y(t) = \frac{0{,}67}{10{,}67}4 \cdot 10^7(1 - e^{-\frac{10{,}67}{4 \cdot 10^7}t})\)
  • Der steady state der Schadstoffmenge \(y(t)\) ist \(\frac{0{,}67}{10{,}67}4 \cdot 10^7 \approx 2{,}51 \cdot 10^6\).
  • Der steady state der Schadstoffkonzentration \(\frac{y(t)}{4\cdot 10^7}\) ist \(\frac{0{,}67}{10{,}67} \approx 0{,}063\).

Wann werden 90 % des steady states erreicht? Antwort: nach ca. 100 Tagen: \[ \begin{aligned} 1 - e^{-\frac{10{,}67}{4\cdot 10^7}t} &= 0{,}9 \\ e^{-\frac{10{,}67}{4\cdot 10^7}t} &= 0{,}1 \\ -\frac{10{,}67}{4\cdot 10^7}t &= \ln(0{,}1) \\ t &= 862314\,\text{Sekunden} \approx 100\,\text{Tage} \end{aligned} \] In Abbildung 2 ist der Verlauf der Konzentration und ihr steady state dargestellt.

Code 
import numpy as np
import matplotlib.pyplot as plt

a = 10.67/4e7
b = 0.67
y0 = 0
t = np.linspace(0,365) # Tage
y_conc = ((y0 - b/a)*np.exp(-a*24*60*60*t) + b/a)/4e7*100  # Konzentration in %
y_conc_steady_state = b/a/4e7*100*np.ones_like(t)  # steady state Konzentration in %

plt.figure(figsize=(4,3))
plt.plot(t, y_conc, label='Zeitverlauf')
plt.plot(t, y_conc_steady_state, '--', label='steady state')
plt.xlabel('Tage')
plt.ylabel('Konzentration (%)')
plt.legend(loc='best')
plt.grid(True)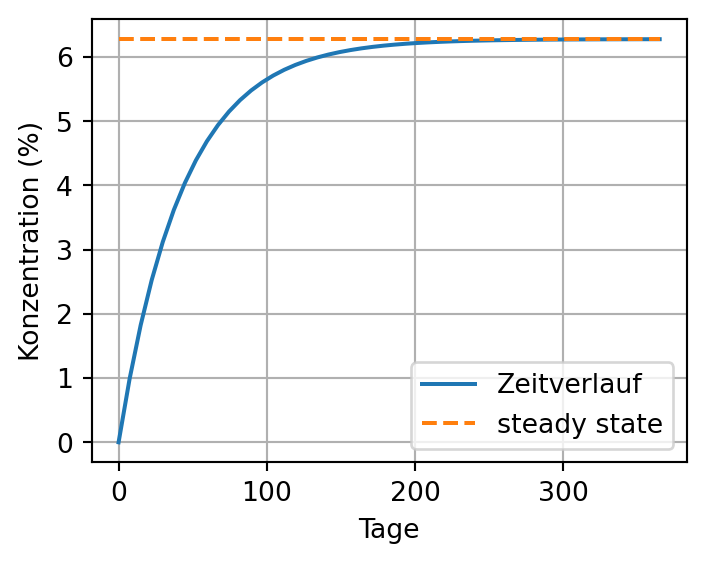
Abbildung 2: Verlauf der Konzentration und ihr steady state

Raumtemperatur

Um Mitternacht beträgt die Raumtemperatur in der FH Vorarlberg 20 °C und außen -5 °C. Die Heizung fällt aus. Zwei Stunden später beträgt die Raumtemperatur nur noch 10 °C. Die Außentemperatur bleibt konstant auf -5 °C. Wir bestimmen den Zeitverlauf der Raumtemperatur. Dazu verwenden wir \(T(t)\) für die Raumtemperatur zum Zeitpunkt \(t\) und \(T_A\) für die Außentemperatur. Newtons Abkühlgesetz besagt, dass \(\dot{T}(t) = -\lambda (T(t) - T_A)\). Wir wissen, dass \(T(0)=20\) und \(T_A=-5\), aber der Parameter \(\lambda\) ist vorerst unbekannt. Die Parameter \(a\) und \(b\) der allgemeinen Form \(\dot{y} + ay = b\) identifizieren wir als \(a=\lambda\) und \(b = \lambda T_A\). Daher lautet die allgemeine Lösung \[ T(t) = \left( T(0)- T_A \right) e^{-\lambda t} + T_A. \] Aus der Bedingung \(T(2)=10\) können wir \(\lambda\) bestimmen: \[ \begin{aligned} 10 &= (20 + 5) e^{-\lambda 2} - 5 \\ 15 &= 25e^{-\lambda 2} \\ e^{-\lambda 2} &= 0.6 \\ -\lambda 2&= \ln(0.6) \\ \lambda &= -0.5\ln(0.6) \approx 0.2554 \end{aligned} \] Die Lösung lautet daher \(T(t) = 25e^{-\lambda t} - 5.\) In Abbildung 3 ist der Verlauf der Raumtemperatur und ihr steady state dargestellt.

Code 
a = -0.5*np.log(0.6)
b = -0.5*np.log(0.6)*(-5)
T0 = 20
t = np.linspace(0, 24)  # Stunden
T = (T0 - b/a)*np.exp(-a*t) + b/a
T_steady_state = b/a*np.ones_like(t)

plt.figure(figsize=(4, 3))
plt.plot(t, T, label='Raumtemperatur')
plt.plot(t, T_steady_state, '--', label='steady state = Aussentemperatur')
plt.xlabel('Stunde nach Mitternacht')
plt.ylabel('Temperatur (°C)')
plt.legend(loc='best')
plt.ylim(-10, 22)
plt.grid(True)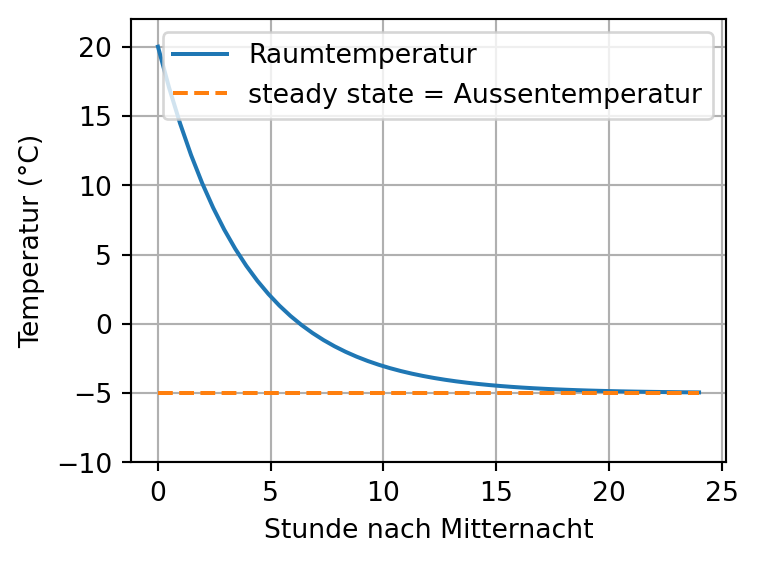
Abbildung 3: Verlauf der Raumtemperatur und ihr steady state

Wann beträgt die Raumtemperatur nur noch 5 °C? \[ \begin{aligned} 5 &= 25e^{-\lambda t} - 5 \\ 10 &= 25e^{-\lambda t} \\ e^{-\lambda t} &= 0{,}4 \\ -\lambda t &= \ln(0{,}4) \\ t &= -\frac{\ln(0{,}4)}{\lambda} \approx 3{,}587 \end{aligned} \] Antwort: ca. \(3{,}6\) Stunden nach Mitternacht.

Allgemeine Schwingungsgleichung und Resonanz

Die DGL einer mechanischen Schwingung und eines elektrischen Schwingkreises lassen sich auf folgende, oft verwendete allgemeine Form bringen: \[ \ddot{y} + 2\delta \dot{y} + \omega_0^2 y = 0. \] Aufgabe: Für welche Werte von \(\delta\) und \(\omega_0\) schwingt das System, d. h. die charakteristischen Gleichung hat komplexe Lösungen? Bestimmen Sie die Frequenz \(\omega\) für diesen Fall.

Lösung: \(\lambda_{1,2} = -\delta \pm \sqrt{\delta^2 - \omega_0^2}\), \(\delta^2 < \omega_0^2\), \(\omega=\sqrt{\omega_0^2 - \delta^2}\). Literatur: z. B. Dietmaier: Mathematik für Angewandte Wissenschaften. p. 440f.

Aufgabe: Für diesen Fall wird die allgemeine Lösung oft in der Form \[ y(t) = e^{-\delta t}[c_1 \cos(\omega t) + c_2 \sin(\omega t)] \] als auch \[ y(t) = Ae^{-\delta t}\cos(\omega t - \varphi) \] geschrieben. Wie hängen diese zwei zusammen? Interpretieren Sie die beiden Formen, und machen Sie Beispielplots.

Lösung: \(c_1 = A\cos(\varphi)\), \(c_2 = A\sin(\varphi)\), Additionstheorem \(\cos(\omega t)\cos(\varphi) + \sin(\omega t)\sin(\varphi) = \cos(\omega t - \varphi)\). Literatur: z. B. Dietmaier: Mathematik für Angewandte Wissenschaften. p. 440f. Abbildung 4 zeigt einen Beispielplot.

Code 
t = np.linspace(0, 10, 500)
A = 2                 # Anfangsamplitude
delta= 0.2            # Dämpfungsfaktor
omega = 2*np.pi/3     # Kreisfrequenz
phi = np.pi           # Phasenverschiebung
y = A*np.exp(-delta*t)*np.cos(omega*t - phi)

plt.figure(figsize=(4, 3))
plt.plot(t, y)
plt.xlabel('t')
plt.ylabel('y')
plt.ylim(-A, A)
plt.grid(True)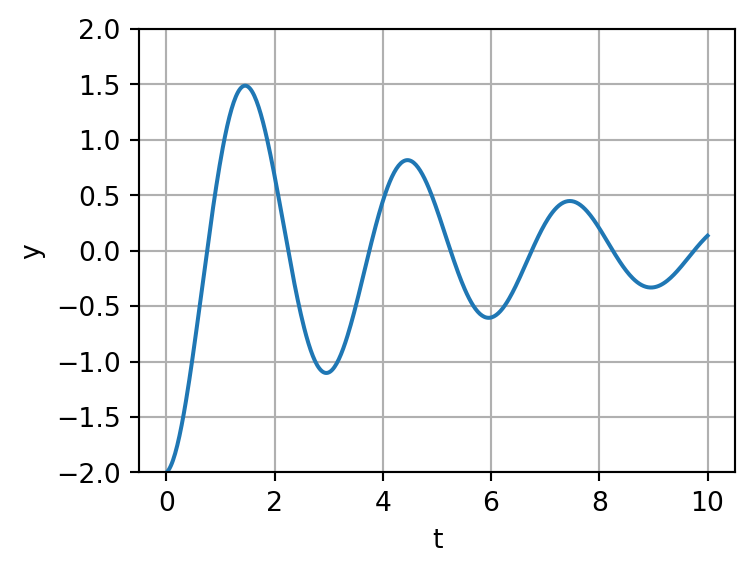
Abbildung 4: Beispiel eines Schwingfalls

Aufgabe: Eine harmonisch erzwungene Schwingung hat die allgemeine Form \[ \ddot{y} + 2\delta \dot{y} + \omega_0^2 y = a\cos(\tilde{\omega}t). \] Eine partikuläre Lösung lautet \[ y_p(t) = A\cos(\tilde{\omega}t - \varphi) \] mit \[ A = \frac{a}{\sqrt{(\omega_0^2 - \tilde{\omega}^2)^2 +4\delta^2\tilde{\omega}^2 }}. \] Bei welchem Wert der Erregerfrequenz \(\tilde{\omega}\) ist die Amplitude \(A\) maximal, d. h. herrscht Resonanz?

Lösung: Ableiten nach \(\tilde{\omega}\) liefert die Resonanzfrequenz \(\omega_r= \sqrt{\omega_0^2 - 2\delta^2} < \omega < \omega_0\). Literatur: Papula: Band2 IV, 4.1.4; Feynman: The Feynman Lectures on Physics, Vol. 1, Chapter 23 Resonance. Abbildung 5 zeigt die Amplitude in Abhängigkeit der Erregerfrequenz.

Code 
delta   = 0.15
omega_0 = 3   # delta < omega_0
omega_t = np.linspace(0, 10, num=500)
a       = 1

A = a/np.sqrt( (omega_0**2 - omega_t**2)**2 + 4*delta**2*omega_t**2 )
omega_r = np.sqrt(omega_0**2 - 2*delta**2)

plt.figure(figsize=(4, 3))
plt.plot(omega_t, A, label='Amplitude A')
y0, y1 = plt.ylim()
plt.vlines(omega_r, y0, y1, linestyle='--', label='Resonanzfrequenz $\omega_r$')
plt.ylim(y0, y1)
plt.xlabel('Erregerfrequenz')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)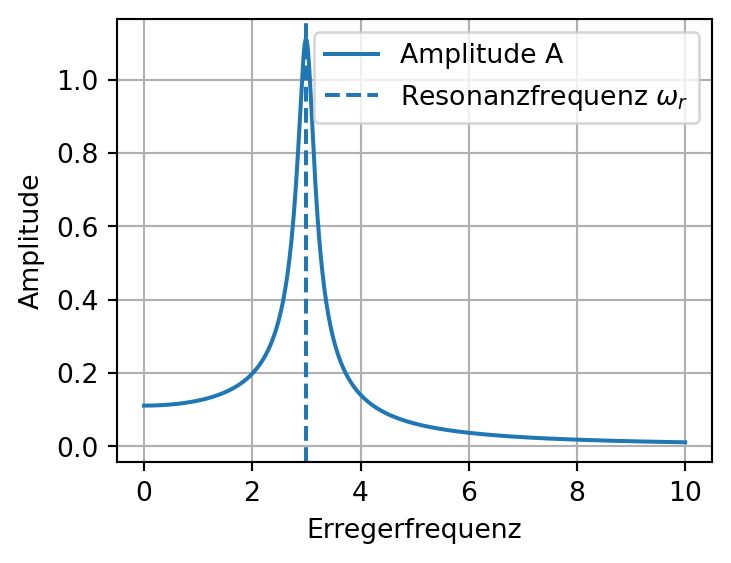
Abbildung 5: Amplitude in Abhängigkeit der Erregerfrequenz

Numerische Lösungen einer DGL

Wir betrachten folgendes Anfangswertproblem: \(y'(x) = \frac{y(x)}{2(x+1)}\) für \(x\geq 0\), Anfangswert \(y(0)=2\).

Analytische Lösung: Die DGL lässt sich mittels Trennung der Variablen lösen, und man erhält für \(x\geq 0\) die allgemeine Lösung \(y(x) = C \sqrt{2(x + 1)}\). Aus der Anfangsbedingung \(y(0)=2\) folgt, dass die Integrationskonstante den Wert \(C=\sqrt{2}\) hat. Die Lösung des Anfangswertproblems lautet daher \(y(x) = 2 \sqrt{x + 1}\). Diese Lösung nennt man eine analytische Lösung. Sie entsteht durch exaktes Umformen des Ausgangsproblems und liefert eine exakte Lösungsformel.

Numerische Lösungen: Oft gelingt es nicht, eine analytische Lösung zu finden, und man versucht, meist am Computer, durch numerische Methoden (d. h. durch Rechnen mit konkreten Zahlenwerten) eine näherungsweise (approximative) Lösung zu berechnen. Das einfachste Verfahren zur numerischen Lösung eines Anfangswertproblems \(\frac{\text{d}y}{\text{d}x} = f(x, y), \;y(x_0) = y_0\) ist das sogenannte Explizite Euler-Verfahren. Für eine Schrittweite \(h>0\) und Schritte \(k = 1, 2, 3, \dotsc\) berechnet man dabei iterativ die folgenden Stützstellen der numerischen Lösung: \[ \begin{aligned} x_k &= x_{k-1} + h \\ y_k &= x_{k-1} + f(x_{k-1}, y_{k-1}) \cdot h \end{aligned} \] Geometrisch wird dabei bei jeder Stützstelle \((x_{k-1}, x_{k-1})\) die Tangente gelegt. Diese hat die Steigung \(f(x_{k-1}, y_{k-1})\). Dann geht man in \(x\)-Richtung einen \(h\)-Schritt weit, folgt dabei der Tangente und kommt so zur nächsten Stützstelle \((x_k, y_k)\). Ein deutlich besseres Verfahren ist in der SciPy-Funktion odeint implementiert.

Vergleich der Methoden: Wir erstellen zuerst in Python einen Plot des Richtungsfeldes der DGL. Anschließend plotten wir die analytische Lösung, berechnen die beiden numerischen Lösungen und zeichnen auch diese diese in den Plot ein, siehe Abbildung 6.

Code 
from scipy.integrate import odeint

x = np.arange(0, 10.5, 0.5)
y = np.arange(0, 8.5, 0.5)
X, Y = np.meshgrid(x, y)

dX = np.ones_like(X)
dY = 0.5*Y/(X+1)

plt.figure(figsize=(5, 5))
plt.quiver(X, Y, dX, dY, headwidth=0.0, scale = 30, pivot = 'middle')
# plt.axis('equal')
plt.xlabel('x')
plt.ylabel('y');
# plt.grid(True)

# exact analytical solution:
x = np.linspace(0, 10)
y_exact = 2*np.sqrt(x + 1)
plt.plot(x, y_exact, '-b', label='exact')

# numerical solutions:
x_0 = 0
y_0 = 2
def my_f(y, x):  
    # Note: inputs must be in order y, x for odeint!
    return 0.5*y/(x+1)

# with Euler:
h = 0.5
x_euler = [x_0]
y_euler = [y_0]
x_k = x_0
y_k = y_0
while x_k < 10:
  y_k = y_k + my_f(y_k, x_k)*h
  x_k = x_k + h
  x_euler.append(x_k)
  y_euler.append(y_k)
plt.plot(x_euler, y_euler, '.-r', label='Euler')

# with odeint:
x = np.linspace(0, 10)
y_odeint = odeint(my_f, y_0, x)
plt.plot(x, y_odeint, '-.y', label='odeint')

plt.legend();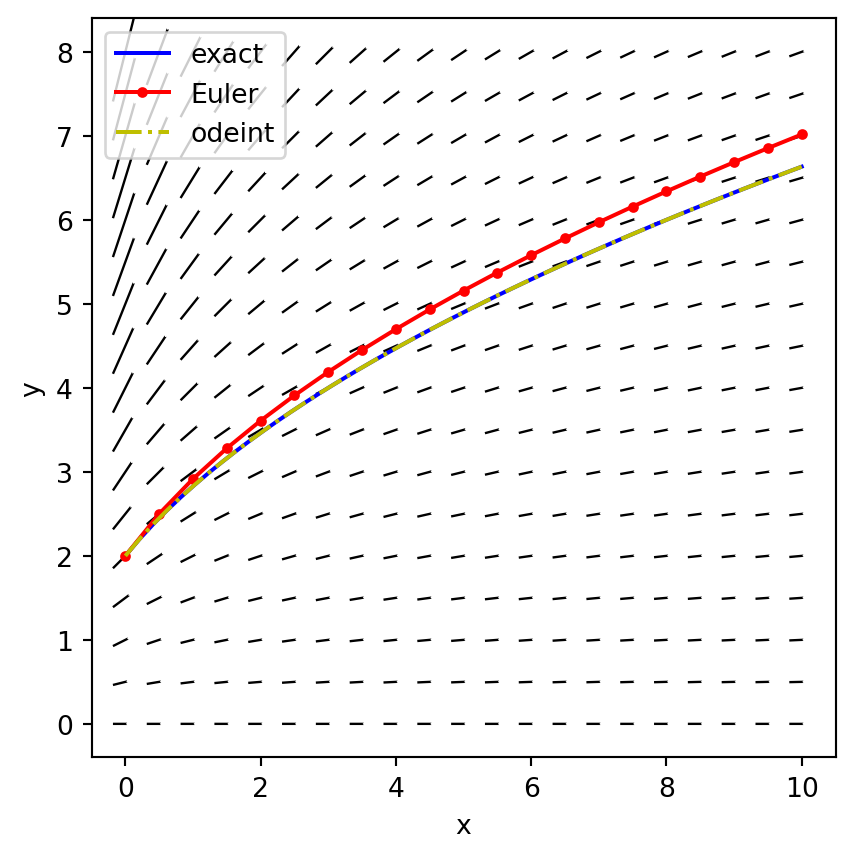
Abbildung 6: Vergleich der analytischen Lösung mit numerischen Lösungen

Aufgaben

Allgemeine und partikuläre Lösung

  1. Zeigen Sie, dass die Funktion \(y(x) = C\frac{x}{1 + x}\) die allgemeine Lösung der Differentialgleichung \(x(1+x)y'(x) - y(x) = 0\) ist. Wie lautet die partikuläre Lösung zum Anfangswert \(y(1)=8\)?
  2. Die Aufladung eines Kondensators der Kapazität \(C\) ab dem Zeitpunkt \(t=0\) über einen ohmschen Widerstand \(R\) auf die Endspannung \(u_0\) erfolgt nach dem Exponentialgesetz \(u_C(t) = u_0 (1- e^{-\frac{t}{RC}})\). Skizzieren Sie die Funktion \(u_C(t)\). Zeigen Sie, dass diese Funktion eine partikuläre Lösung der Differentialgleichung \(RC\dot{u_C}(t) + u_C(t) = u_0\) ist, die diesen Einschaltvorgang beschreibt. Erstellen Sie in Python Plots der Funktion \(u_C(t)\) für verschiedene Werte von \(C\) und \(R\).

Quellen:

  1. [1], Kapitel IV Gewöhnliche Differentialgleichungen, Übungsaufgaben zu Abschnitt 1, Aufgabe 1
  2. [1], Kapitel IV Gewöhnliche Differentialgleichungen, Übungsaufgaben zu Abschnitt 1, Aufgabe 3

Trennung der Variablen

Lösen Sie folgenden DGL mit der Methode der Trennung der Variablen.

  1. \(y\dot{y} = te^t\)
  2. \(\dot{y}(1 + t^2) = ty\)
  3. \(y' = 5x^4(y + 1)\)

Quellen:

  1. [2] S. 516
  2. [1] S. 520
  3. [1] Kapitel IV, Abschnitt 2, Aufgabe 20e

Allgemeine Lösung

Bestimmen Sie die allgemeine Lösung der Differentialgleichung \(y'(x) = \frac{x^2 + 2}{y}.\)

Quelle: [3] p. 23, problem 4.3

Anfangswertprobleme

Lösen Sie die folgenden Anfangswertprobleme:

  1. \(yy' = \cos(2x), \; y(0) = -1\).
  2. \(y' = \frac{-x}{y}, \; y(0)=1.\)
  3. \(y' + \cos(x)\, y = 0, \quad y(\pi/2) = 2\pi\)

Substitution 1

Lösen Sie das Anfangswertproblem \(yy' = x + \frac{y^2}{x}, \quad y(1) = \sqrt{2}\) mittels einer geeigneten Substitution.

Quelle: [1] Kapitel IV, Abschnitt 2, Aufgabe 3

Substitution 2

Lösen Sie das Anfangswertproblem \(x^2y' = y^2 + xy, \; y(1)=-1\) mittels einer geeigneten Substitution.

Quelle: [1] Kapitel IV, Abschnitt 2, Aufgabe 6a

Gemischte Aufgaben

Lösen Sie die folgenden DGL, und machen Sie die Probe.

  1. \(y' = -\frac{x^2}{y^3}\), \(y(0) = 1\).
  2. \(y' = \frac{\sin^2(x)}{y}\), \(y(\pi/2) = 0\).
  3. \(y' = \sinh(x + y) + \cosh(x + y)\), Hinweis: Stellen Sie die hyperbolischen Funktionen als Exponentialfunktionen dar.

Bewegung eines Körpers

Ein Körper bewegt sich entlang der positiven \(x\)-Achse. Zur Zeit \(t=0\) befindet er sich im Punkt \(x=10\) m. Die Bewegung erfolgt so, dass das Produkt aus Ort \(x(t)\) und Geschwindigkeit \(\dot{x}(t)\) konstant 10 m\(^2\)/s ist. Berechnen Sie den Ort \(x(t)\) und die Geschwindigkeit \(\dot{x}(t)\) als Funktionen der Zeit \(t\).

Quadratischer Luftwiderstand

Ein Auto mit Masse \(m\) und Anfangsgeschwindigkeit \(v_0\) bewegt sich nur unter dem Einfluss des als quadratisch von der Geschwindigkeit abhängig angenommenen Luftwiderstands.

  1. Erklären Sie, warum die Geschwindigkeit \(v(t)\) des Autos die DGL \(\dot{v}(t) = -\frac{c}{m}v(t)^2\) erfüllt.
  2. Lösen Sie das Anfangswertproblem und erstellen Sie einen Plot der Lösung in Python für vernünftige Werte der Parameter.

Menge an \(CO_2\) in einem Raum

Die Luft in einem Raum voller Menschen enthält im Volumenanteil 0,25 % Kohlendioxid (\(CO_2\)). Eine Klimaanlage wird eingeschaltet und bläst mit einer Geschwindigkeit von 500 Kubikmeter pro Minute Frischluft in den Raum. Die frische Luft vermischt sich mit der verbrauchten Luft, und das Gemisch verlässt den Raum mit einer Geschwindigkeit von 500 Kubikmeter pro Minute. Die frische Luft enthält 0,01 % \(CO_2\), und der Raum hat ein Volumen von 2500 Kubikmetern.

  1. Bestimmen Sie die DGL, die das Volumen \(y(t)\) an \(CO_2\) im Raum zu jedem Zeitpunkt \(t\) erfüllt. Lösen Sie das Anfangswertproblem, und machen Sie einen Plot der Lösung in Python.
  2. Das in 1. entwickelte Modell ignoriert das durch die Atmung der Personen im Raum erzeugte \(CO_2\). Nehmen wir an, dass die Menschen im Raum 0,08 Kubikmeter \(CO_2\) pro Minute produzieren. Berücksichtigen Sie in einer neuen DGL diese zusätzliche \(CO_2\)-Quelle. Lösen Sie das Anfangswertproblem, und machen Sie einen Plot der Lösung in Python zum Vergleich mit der Lösung in 1..

Quelle: [2] p.546, Exercise 21

Linearer Luftwiderstand 1

Eine Person mit einer Masse von 70 kg springt mit einem offenen Fallschirm ohne Anfangsgeschwindigkeit aus einer Höhe von 1000 m. Die Luftwiderstandskraft sei gleich \(140v(t)\) Newton, wobei \(v(t)\) die Geschwindigkeit der Person in Metern pro Sekunde bezeichnet.

  1. Bestimmen Sie die DGL für \(v(t)\). Lösen Sie das Anfangswertproblem und erstellen Sie einen Plot der Lösung in Python.
  2. Bestimmen Sie die Grenzgeschwindigkeit und graphisch die Zeit bis zum Bodenkontakt.

Quelle: [3] p.60, Exercise 7.12

Linearer Luftwiderstand 2

Ein Körper mit einer Masse von 2 kg fällt mit einer anfänglichen Sinkgeschwindigkeit von 4 m/s aus einer Höhe von 1000 m. Die Luftwiderstandskraft sei proportional zu seiner Geschwindigkeit, und seine daraus resultierende Grenzgeschwindigkeit (steady state) sei 40 m/s. Bestimmen Sie seine Geschwindigkeit als Funktion der Zeit und seinen Ort als Funktion der Zeit. Verwenden Sie für die Erdbeschleunigung den Wert 10 m/s\(^2\)

Quelle: [3] p. 61f, problem 7.13

RL Schaltung

Die DGL, die die elektrische Stromstärke \(I(t)\) (A) zu einem Zeitpunkt \(t\) (s) in einer RL-Schaltung beschreibt, ist gegeben durch \[ L\dot{I} + RI = U, \] wobei \(R\) (\(\Omega\)) den Widerstand, \(L\) (H) die Induktivität und \(U\) (V) die Spannung ist. Eine gegebene Schaltung habe eine Spannung von 5 V, einen Widerstand von 50 \(\Omega\), eine Induktivität von 1 H sowie anfangs eine Stromstärke \(I(0)=0\). Berechnen Sie die Stromstärke \(I(t)\) für \(t\geq 0\), und erzeugen Sie einen Plot der Lösung in Python.

Quelle: [3] p.52, p.65, Exercise 7.19

Lineare DGL 1. Ordnung mit variablen Koeffizienten 1

Lösen Sie die DGL \(\dot{y}(t) +t y(t) = 4t\).

Lineare DGL 1. Ordnung mit variablen Koeffizienten 2

Lösen Sie das Anfangswertproblem \(y' + \frac{1}{x}y = \frac{\ln(x)}{x}\) und \(y(1) = 1\) für \(x > 0\).

Quelle: [1] Kapitel IV, Abschnitt 2: 16c

Lineare DGL 1. Ordnung mit variablen Koeffizienten 3

Lösen Sie die Anfangswertaufgabe \(xy' - y = x^2\cos(x),\; y(\pi) = 2\pi\) für \(x > 0\).

Quelle: [1] Kapitel IV, Abschnitt 2: 16a

Lineare DGL 1. Ordnung mit variablen Koeffizienten 4

Lösen Sie die folgenden DGL bzw. Anfangswertprobleme.

  1. \(y' - y = e^x\), \(y(1) = 0\).
  2. \(y' - \frac{2}{x}y = x^2 e^x\)
  3. \(y' + \tan(x)y = 2x\cos(x)\), \(y(0) = -1\).
  4. \(y' + \cot(x)y = 5e^{\cos(x)}\)

Lineare DGL 1. Ordnung mit variablen Koeffizienten 5

Lösen Sie die folgende DGL, und machen Sie die Probe. \[ y' + \sin(x)y = \sin^3(x) \]

Lineare DGL 1. Ordnung mit variablen Koeffizienten 6

Lösen Sie die folgende nicht-lineare DGL mit \(k \in \mathbb{R}\), indem Sie sie mittels der Substitution \(u(x) = e^{y(x)}\) in eine lineare DGL transformieren, und machen Sie die Probe. \[ e^y y' = k(x + e^y) - 1 \]

Newtonsches Abkühlungsgesetz 1

Eine hungrige Studentin schaltet den Ofen ein und legt eine kalte Pizza aufs Blech, ohne den Ofen vorzuheizen. Sei \(T_P(t)\) die Temperatur der Pizza und \(T_O(t)\) die Ofentemperatur (°C) jeweils \(t\) Minuten, nachdem der Ofen eingeschaltet wurde. Nach dem Newtonschen Abkühlungsgesetz ist die Temperaturänderungsrate proportional zur Temperaturdifferenz von Pizza zu Ofen: \[ \dot{T_P}(t) = - k[T_P(t) - T_O(t)], \] wobei \(k\) eine positive Konstante ist. Angenommen die Ofentemperatur ist für \(0\,\text{min} \leq t \leq 8\,\text{min}\) gegeben durch \(T_O(t)= 20 + 30t\), mit \(k= 0.1\,\text{min}^{-1}\) und einer anfänglichen Pizzatemperatur von 4°C.

  1. Bestimmen Sie die Temperatur der Pizza in den ersten 8 Minuten.
  2. Plotten Sie die Temperatur der Pizza über die ersten 8 Minuten.

Quelle: [2] p. 526f

Newtonsches Abkühlungsgesetz 2

Ein Körper mit einer unbekannten Temperatur wird in einen Raum mit konstanter Umgebungstemperatur von 30 °C platziert. Nach 10 Minuten ist die Temperatur des Körpers 0 °C und nach 20 Minuten ist sie 15 °C. Bestimmen Sie die unbekannte Anfangstemperatur.

Hinweis: Newtonschen Abkühlungsgesetz \(\dot{T}(t) = - k[T(t) - T_U]\)

Quelle: [3] Aufgabe 7.10, S. 59

Solarthermie

Das Heizungssystem eines Gebäudes bestehe aus Solarkollektoren und einem Warmwasserspeicher. Der Warmwasserspeicher habe eine Zeitkonstante von \(\frac{1}{k} = 50\) Stunden, d. h. er kühlt ohne Wärmezufuhr nach dem Newtonschen Abkühlungsgesetz \(\dot{T}(t) = - k[T(t) - T_U(t)]\) aus, wobei \(T_U(t)\) die Umgebungstemperatur zur Stunde \(t\) ist. Der solare Eintrag führt pro Stunde zu einer Temperaturerhöhung um 2 °C im Speicher. Um 9 Uhr morgens (\(t=0\)) habe der Speicher eine Wassertemperatur von 30 °C und die Umgebungstemperatur sei den ganzen Tag über bei 20 °C.

  1. Stellen Sie die Differentialgleichung inkl. Anfangsbedingung auf, die den Temperaturverlauf des Warmwasserspeichers bei Sonneneinstrahlung ab 9 Uhr beschreibt.
  2. Lösen Sie dieses Anfangswertproblem.

Quelle: [4] Section 2.5, Problem 14, p. 76.

Elektroautobatterie

Das Elektroauto Think City verfügt über eine Zebra-Batterie (Natrium-Nickelchlorid) mit einer maximalen Lade- und Entladeleistung von \(P_{\text{max}} = 30\) kW und einer Kapazität von \(E_{\text{max}} = 20\) kWh. Ein elektrischer Widerstand in der Batterie wandelt elektrische Energie in Wärme um, die die Batterie während dem Laden und Entladen auf Betriebstemperatur hält. Dieser Widerstand und folglich auch die resultierenden thermischen Verluste hängen linear vom momentanen Ladezustand der Batterie ab, bei einer Verlustleistung von minimal \(I_{\text{min}} = 40\) W und maximal \(I_{\text{max}} = 120\) W. Die in der Batterie gespeicherte Energie kann demnach für \(E(t) > 0\) beschrieben werden durch: \[ \dot{E}(t) = -I_{\text{max}} + \frac{I_{\text{max}} - I_{\text{min}}}{E_{\text{max}}} E(t) + P(t) \]

  1. Skizzieren Sie die thermischen Verluste in Abhängigkeit der gespeicherten Energie und erklären Sie die Differentialgleichung.
  2. Lösen Sie das Anfangswertproblem \(E(0) = 10\) kWh bei einer konstanten Ladeleistung von \(P = 20\) kW. Wann ist die Batterie vollständig geladen?
  3. Bei einer konstanten Entladeleistung von \(P = -10\) kW, wie hoch ist der Energieinhalt der Batterie nach einer Stunde, wenn die Batterie zu Beginn voll geladen war?

Mischung

Ein Tank enthält ursprünglich 200 Liter reines Wasser. Eine Salzlösung mit 1 kg Salz pro 4 Liter Wasser wird bei einer Rate von 12 Liter pro Minute in den Tank eingebracht. Salz und Wasser durchmischen sich perfekt, und 12 Liter der Mischung fließen pro Minute wiederum aus dem Tank heraus.

  1. Stellen Sie die Differentialgleichung auf, die die Menge (in kg) an Salz im Tank über die Zeit hinweg beschreibt.
  2. Lösen Sie diese Differentialgleichung.
  3. Bestimmen Sie, falls vorhanden, den steady state.
  4. Skizzieren Sie die Lösung.

Quelle: [4] Example 1, p. 61f.

Aufladen eines Kondensators

Das Aufladen eines Kondensators mit der Kapazität \(C\) über einen ohmschen Widerstand \(R\) wird durch die lineare Differentialgleichung \[ RC \dot{u_C}(t) + u_C(t) = u(t) \] beschrieben. Dabei ist \(u(t)\) die von außen angelegte Spannung und \(u_C(t)\) die Spannung am Kondensator.

  1. Bestimmen Sie die allgemeine Lösung der Differentialgleichung bei einer konstanten äußeren Spannung \(u(t) = u_0\).
  2. Wie lautet die Lösung für den Anfangswert \(u_C(0) = 0\)? Skizzieren und beschreiben Sie die Lösung.

Quelle: [1] Kapitel IV, Abschnitt 2, Aufgabe 26

Lineare DGL 2. Ordnung 1

Lösen Sie die Differentialgelichung \(\ddot{y} + 3\dot{y} + 2y = 0\) mit den Anfangsbedingungen \(y(0) = 2\) und \(\dot{y}(0)= -3\).

Lineare DGL 2. Ordnung 2

Bestimmen Sie die Lösungen folgender GDGL bzw. Anfangswertprobleme. Beschreiben Sie die Lösungen und deren Verhalten für \(x \rightarrow \infty\).

  1. \(y''(x) + 5y'(x) - 6y(x) = 0\)
  2. \(y''(x) - y(x) = 0\), \(y(0)=1\) und \(y'(0)= 0\)

Quelle: [4] Sec. 3.4., Example 1, p. 131f.

Lineare DGL 2. Ordnung 3

Wir betrachten die GDGL \(y''(x) - 2y'(x) + y(x) = e^{3x}\).

  1. Zeigen Sie, dass \(\frac{1}{4}e^{3x}\) eine partikuläre Lösung ist.
  2. Bestimmen Sie die allgemeine Lösung.

Quelle: [3] Aufgabe 8.23, S. 79.

Lineare DGL 2. Ordnung 4

Bestimmen Sie die Lösungen folgender Anfangswertprobleme und beschreiben Sie die Lösungen und deren Verhalten für \(x \rightarrow \infty\).

  1. \(y''(x) + 6y'(x) + 9y(x) =0\), \(y(0)=1\) und \(y'(0)= 2\)
  2. \(y''(x) + 8y'(x) + 20y(x) =0\), \(y(0)=1\) und \(y'(0)= 6\)

Quelle: [5] p. 474, Aufgaben 12.9 b und c

Mehr Aufgaben

  • [1] Kapitel IV

    • Abschnitt 1, Aufgaben 1 - 4
    • Abschnitt 2, Aufgaben 1 - 10, 13 - 28
    • Abschnitt 3, Aufgaben 1 - 14

  • [6] Kapitel G Gewöhnliche Differentialgleichungen

    • Abschnitt 1 Differentialgleichungen 1. Ordnung: G1 - G44
    • Abschnitt 2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten: G53 - G71

  • [7] Kapitel IX Gewöhnliche Differentialgleichungen: Beispiele 1 - 16

Literatur

[1]
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler Band 2: Ein Lehr- und Arbeitsbuch für das Grundstudium, 14., überarb. u. erw. Aufl. Wiesbaden: Springer Vieweg, 2015.
[2]
L. J. Goldstein, D. I. Schneider, D. C. Lay, und N. H. Asmar, Calculus & Its Applications, 14, Global Edition. Pearson Education Limited, 2018.
[3]
R. Bronson und G. Costa, Schaum’s Outline of Differential Equations (Schaum’s Outlines), 4. Auflage. Mcgraw-Hill Education Ltd, 2014.
[4]
S. J. Farlow, An Introduction to Differential Equations and Their Applications, Illustrated Edition. Mineola, N.Y: Dover, 2006.
[5]
C. Dietmaier, Mathematik für angewandte Wissenschaften, 2014. Aufl. Berlin Heidelberg: Springer Spektrum, 2014.
[6]
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler - Klausur- und Übungsaufgaben: 711 Aufgaben mit ausführlichen Lösungen zum Selbststudium und zur Prüfungsvorbereitung, 6., erw. u. überarb. Aufl. 2020 Edition. Wiesbaden: Springer Vieweg, 2020.
[7]
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler - Anwendungsbeispiele: 222 Aufgabenstellungen mit ausführlichen Lösungen, 8., überarb. Aufl. Wiesbaden Heidelberg: Springer Vieweg, 2019.