Assignment #06

#06-01: Use datetime provided in WX

Load WX_GNP.csv, the same data set we used in last unit’s assignment.
How many records are available from 2019?
Create a new data frame WX19 that contains all records from the 2018/19 winter season. Let’s take all records between September and Mai. The only meteorological variables we need in addition to the meta variables station_id and datetime are ta and iswr.
Save WX19 as a new csv file.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

WX = pd.read_csv("../05_files/WX_GNP.csv", sep=",", parse_dates=["datetime"])
WX

	datetime	station_id	hs	hn24	hn72	rain	iswr	ilwr	ta	rh	vw	dw	elev
0	2019-09-04 06:00:00	VIR075905	0.000	0.000000	0.00000	0.000000	0.000	256.326	6.281980	94.7963	2.32314	241.468	2121
1	2019-09-04 17:00:00	VIR075905	0.000	0.000000	0.00000	0.000196	555.803	288.803	12.524600	72.0814	4.38687	247.371	2121
2	2019-09-05 17:00:00	VIR075905	0.000	0.000000	0.00000	0.000045	534.011	287.089	14.265400	55.1823	1.93691	239.254	2121
3	2019-09-06 17:00:00	VIR075905	0.000	0.000000	0.00000	0.000026	546.008	292.024	14.136600	72.5560	3.67782	239.715	2121
4	2019-09-07 17:00:00	VIR075905	0.000	0.000000	0.00000	0.000150	528.582	289.508	14.623800	68.9262	1.90232	227.356	2121
...	...	...	...	...	...	...	...	...	...	...	...	...	...
178733	2021-05-25 17:00:00	VIR088016	279.822	2.197360	7.07140	0.108814	346.135	314.824	2.471430	94.4473	1.28551	170.356	2121
178734	2021-05-26 17:00:00	VIR088016	272.909	0.000000	1.73176	0.001291	747.383	256.193	5.066340	78.2142	4.11593	208.909	2121
178735	2021-05-27 17:00:00	VIR088016	267.290	2.412910	2.80912	0.167091	185.431	316.157	1.090880	97.3988	4.65204	218.963	2121
178736	2021-05-28 17:00:00	VIR088016	275.573	11.509200	12.80780	0.000000	269.329	308.515	0.247583	88.5444	5.33803	263.788	2121
178737	2021-05-29 17:00:00	VIR088016	267.562	0.259779	6.15200	0.000766	766.358	247.267	4.666620	69.3598	1.92538	256.041	2121

178738 rows × 13 columns

sum(WX['datetime'].dt.year == 2019)

or less elegant, but conceptually simpler

WX[(WX['datetime'] >= pd.to_datetime('2019-01-01')) & (WX['datetime'] < pd.to_datetime('2020-01-01'))].shape[0]

WX19 = WX.loc[
    (WX['datetime'] >= pd.to_datetime('2018-09-01')) & (WX['datetime'] < pd.to_datetime('2019-06-01')),
    ['datetime', 'station_id', 'ta', 'iswr']
].copy()
print(f"There are {len(WX19['datetime'].unique())} unique time stamps between '{WX19['datetime'].min()}' and '{WX19['datetime'].max()}'.")

There are 239 unique time stamps between '2018-09-05 06:00:00' and '2019-04-30 17:00:00'.

or alternatively using datetime components:

WX19 = WX.loc[
    ((WX['datetime'].dt.year == 2018) & (WX['datetime'].dt.month >= 9)) | 
    ((WX['datetime'].dt.year == 2019) & (WX['datetime'].dt.month <= 5)),
    ['datetime', 'station_id', 'ta', 'iswr']
].copy()
print(f"There are {len(WX19['datetime'].unique())} unique time stamps between '{WX19['datetime'].min()}' and '{WX19['datetime'].max()}'.")

There are 239 unique time stamps between '2018-09-05 06:00:00' and '2019-04-30 17:00:00'.

WX19.to_csv("WX19.csv", index=False)

#06-02: Quick ’n dirty time series

From WX19, create a new data frame WXzoom1 that contains the records from the first two weeks of January and any station_id of your choice.
Using the WXzoom1 data frame, plot a line graph of the temperature that also shows the measurements with circles and, in a different figure, plot an area curve of the incoming shortwave radiation.

WXzoom1 = WX19.loc[
    (WX19['datetime'].dt.dayofyear <= 14) & (WX19['station_id'].isin(["VIR075905"])),
    ['datetime', 'station_id', 'ta', 'iswr']
].copy()
WXzoom1

	datetime	station_id	ta	iswr
57477	2019-01-01 17:00:00	VIR075905	-7.78452	111.1250
57478	2019-01-02 17:00:00	VIR075905	-7.09891	72.2500
57479	2019-01-03 17:00:00	VIR075905	-3.90653	27.7500
57480	2019-01-04 17:00:00	VIR075905	-4.25220	33.3125
57481	2019-01-05 17:00:00	VIR075905	-4.86277	100.0000
57482	2019-01-06 17:00:00	VIR075905	-8.70954	83.3750
57483	2019-01-07 17:00:00	VIR075905	-9.06894	44.4375
57484	2019-01-08 17:00:00	VIR075905	-11.57240	61.1250
57485	2019-01-09 17:00:00	VIR075905	-6.33497	61.1250
57486	2019-01-10 17:00:00	VIR075905	-3.93680	122.2500
57487	2019-01-11 17:00:00	VIR075905	-5.83427	133.3750
57488	2019-01-12 17:00:00	VIR075905	-5.70246	144.4380
57489	2019-01-13 17:00:00	VIR075905	-5.11887	144.4440
57490	2019-01-14 17:00:00	VIR075905	-6.42997	155.6250

WXzoom1.set_index('datetime', inplace=True)

WXzoom1['ta'].plot(marker="o")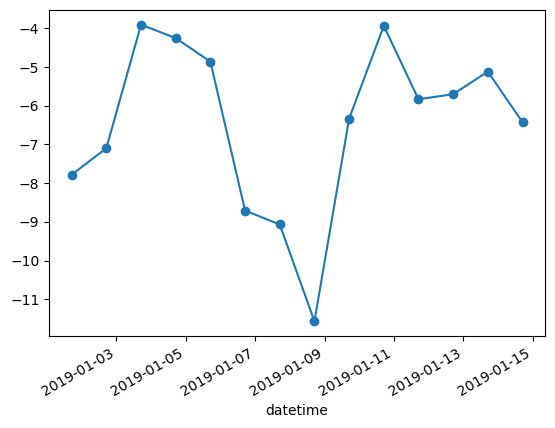

WXzoom1['iswr'].plot.area()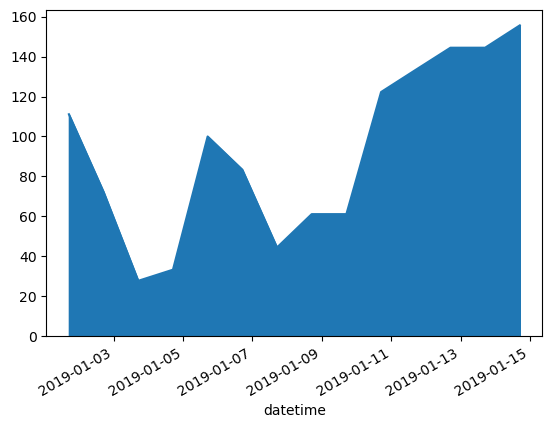

#06-03: Summary stats

From WX19, create a new data frame WXzoom2 that contains the records from the first two weeks of January and the first two station_id’s in WX19['station_id'].unique().
Using the WXzoom2 data frame, what is the average temperature of each of the stations?
Using the WXzoom2 data frame, plot the temperature curves of both stations into one figure.

WXzoom2 = WX19.loc[
    (WX19['datetime'].dt.dayofyear <= 14) & (WX19['station_id'].isin(WX19["station_id"].unique()[:2])),
    ['datetime', 'station_id', 'ta', 'iswr']
].copy()
WXzoom2.set_index('datetime', inplace=True)

WXzoom2.groupby("station_id")["ta"].mean()

station_id
VIR075905   -6.472368
VIR075906   -5.492010
Name: ta, dtype: float64

or alternatively, you can manually extract the values of all stations or use a loop:

for station in WXzoom2["station_id"].unique():
    print(f"{station}: {WXzoom2.loc[WXzoom2['station_id'] == station, 'ta'].mean():.4f}")

VIR075905: -6.4724
VIR075906: -5.4920

fig, axs = plt.subplots()
WXzoom2["ta"][WXzoom2["station_id"] == WXzoom2["station_id"].unique()[0]].plot(ax=axs)  # mind the `ax` argument to tell Pandas in where to plot this to
WXzoom2["ta"][WXzoom2["station_id"] == WXzoom2["station_id"].unique()[1]].plot(ax=axs)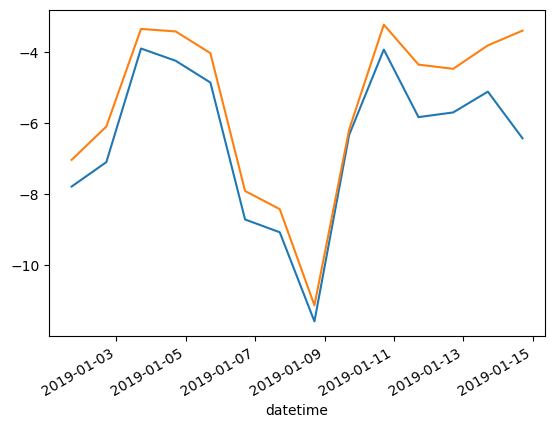

or alternatively, using a clever way of re-shaping the data frame from a long to a wide format, and making use of the fact that every column will become its own artist on the plot.

WXzoom2.pivot(columns="station_id", values="ta").plot()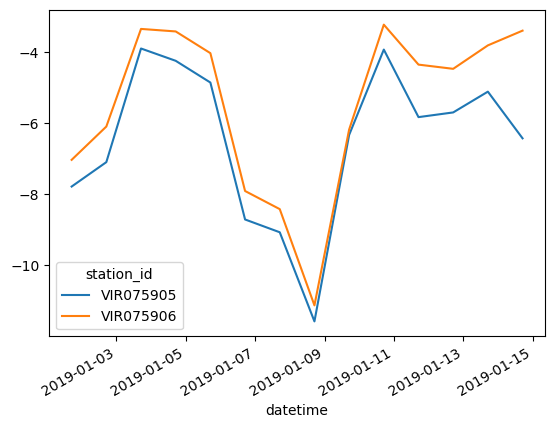

alternatively, you can achieve the same result with a loop. This will yield a much more inefficient computation, though, and also the plot will have to be adjusted (e.g., using ta_dt as x axis instead of ta_lower.index):