Correction of 2nd exam 2023/24

NES—Programmiertechniken (Introduction to scientific programming)

12.03.2024

Please work through the following tasks. You have 75 minutes to complete the exam.
Make sure you executed all relevant code cells and save the notebook before the end of the exam.

This is a correction of the exam questions. Like always in programming, there are many ways to achieve similar results. My suggestions here follow our coding exercises discussed in class.

If you want to solve this exam as an exercise, download the uncorrected notebook.

import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Question 1: Multiple-choice (5 points)

To tick correct answers, replace - [ ] with - [x]

Careful: wrongly ticked answers will give negative points!

(a) Which of the following statements are true? (2.5 points)

A python script with the file ending .py can be run from the terminal with the python command.
conda can be used to install software required to use python on laptops.
A terminal cannot run a python interpreter.
Imagine you work on different work/research projects using python that rely on different packages. In this case it is a good idea to keep the software installation of python and its packages in separate conda environments, one for each project.
Using the terminal is an outdated form of communicating with the computer. Nowadays, every task can be done with graphical user interfaces and sophisticated programs.

(b) Which of the following statements are true? (2.5 points)

Logical indexing is a vectorized notation that can replace explicit for loops in python.
Each python script or program has exactly one namespace.
In python, not all container data types are mutable.
If a function modifies and then returns its input parameters, it is said to cause side effects, which should generally be avoided.
The break statement is used to terminate a python program.

Question 2: datetime calculations (6 points)

Create a DataFrame df with a DatetimeIndex ranging from 2024-01-01 to 2024-12-31 in daily sampling. (1 point)

df = pd.DataFrame(index=pd.date_range('2024-01-01', '2024-12-31', freq='D'))

Create a column named day_of_year that stores the day of the year from 1 to however many days there are in 2024. (1 point)

df['day_of_year'] = df.index.day_of_year
# df['day_of_year'] = np.arange(1, df.shape[0]+1)  # alternative solution without `index`

Create another column squared that computes the square of day_of_year (i.e., day_of_year to the power of two.) (0.5 points)

df['squared'] = df['day_of_year']**2

At which date is squared equal to 3600? (1 point)

df.index[df['squared'] == 3600]

DatetimeIndex(['2024-02-29'], dtype='datetime64[ns]', freq='D')

Resample the Series squared to their monthly minimum and maximum values and plot them in a quick working plot.
The code cell for this task should contain a maximum of five lines. (2.5 points)

dfr = pd.DataFrame()
dfr['max'] = df['squared'].resample('M').max()
dfr['min'] = df['squared'].resample('M').min()
dfr.plot()

## Alternative solution:
# dfr1 = df['squared'].resample('M').min()
# dfr2 = df['squared'].resample('M').max()
# fig, ax = plt.subplots()
# dfr1.plot(ax=ax)
# dfr2.plot(ax=ax)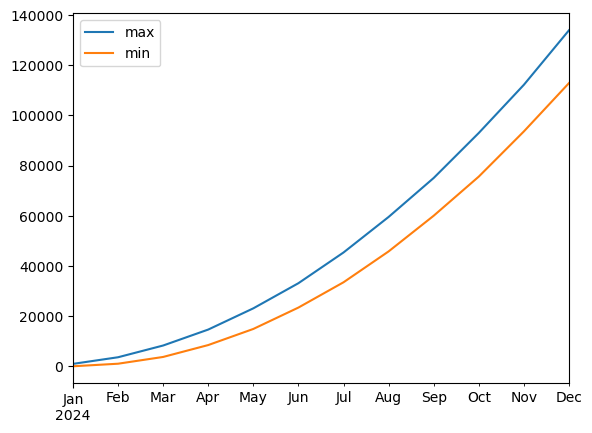

Question 3: Spreadsheet data (9 points)

Your working directory contains a spreadsheet dataset.csv.
Solve the following tasks:

Load the data contained in the spreadsheet dataset.csv. (1 point)

xyvc = pd.read_csv('dataset.csv', sep=';')

How many different classes are contained in the data set and what are their names? (1 point)

cls = xyvc['class'].unique()
print(f'There are {len(cls)} unique classes named {cls}')

There are 4 unique classes named ['cold' 'very hot' 'hot' nan]

It looks like there are some NaN’s in the DataFrame. How many are there in each column? (1 point)

xyvc.isna().sum()

x        0
y        0
value    0
class    3
dtype: int64

Set the value for each class that is NaN to 120. (1 point)

xyvc.loc[xyvc['class'].isna(), 'value'] = 120

Extract the average value of each class and compute the standard deviation of the resulting vector.
There are several ways to achieve this. If you are unsure, implement the solution with a loop. (2.5 points)

## Strategy 1: loop
avg_val_list = []
for cl in xyvc['class'].unique():
    avg_val_list.append(xyvc.loc[xyvc['class'].isin([cl]), 'value'].mean())

avg_val_arr = np.array(avg_val_list)
std = avg_val_arr.std()

## Strategy 2: vectorized using groupby
# avg_val = xyvc.groupby(['class']).mean()
# std = avg_val['value'].std()
# std

## Note that the result between the two solutions differ because of different implementations of the std method in numpy versus pandas.
## (They assume different degrees of freedom per default. Pass ddof=1 and they will agree.)
## The actual result does influence the points you will achieve on this task!

print(std)

44.914185064187755

Use the .pivot() method to convert the DataFrame from a long format to a wide format.
x and y become the columns and the index, while the cells should be filled with the value column. (1 point)

wide = xyvc.pivot(columns='x', index='y', values='value')
wide

x	-5	-4	-3	-2	-1	0	1	2	3	4
y
10	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
11	100.0	74.346826	63.876045	58.754101	55.876734	54.126183	53.039461	120.000000	52.103272	52.103272
12	100.0	83.517533	72.415588	65.281601	60.649651	57.615778	55.661765	120.000000	53.943350	53.943350
13	100.0	87.319512	77.010354	69.340846	63.867714	60.076707	57.557361	120.000000	55.298757	55.298757
14	100.0	88.766049	78.996704	71.249228	65.461889	61.334948	58.544683	56.829710	56.015313	56.015313
15	100.0	88.766049	78.996704	71.249228	65.461889	61.334948	58.544683	56.829710	56.015313	56.015313
16	100.0	87.319512	77.010354	69.340846	63.867714	60.076707	57.557361	56.023649	55.298757	55.298757
17	100.0	83.517533	72.415588	65.281601	60.649651	57.615778	55.661765	54.491880	53.943350	53.943350
18	100.0	74.346826	63.876045	58.754101	55.876734	54.126183	53.039461	52.400447	52.103272	52.103272
19	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000

Using the wide DataFrame, re-create the following Figure as closely as possible (incl. labels). (2.5 points)

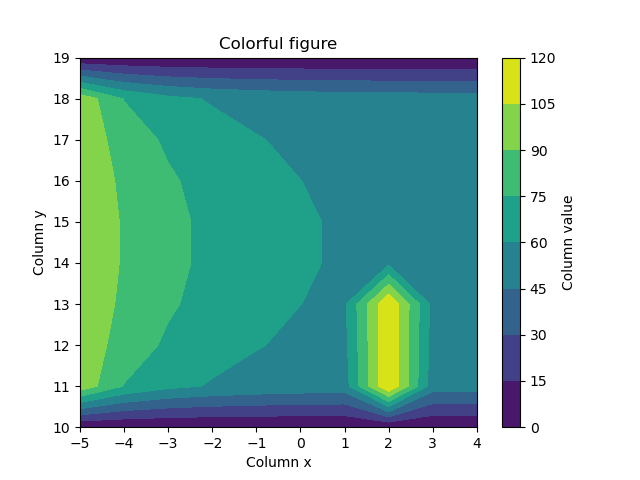
fig, ax = plt.subplots()
ct = plt.contourf(wide.columns, wide.index, wide)
cbar = plt.colorbar(ct)
ax.set_ylabel('Column y')
ax.set_xlabel('Column x')
cbar.set_label('Column value')
ax.set_title("Colorful figure")
plt.show()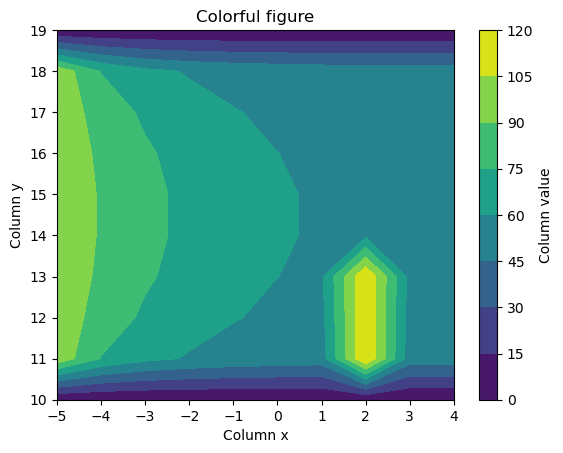

Question 4: Code snippets! (7 points)

(a) Loop with user input:

The following code block misses some code. Fill in the gaps where indicated by the comments. (2 points)

numbers = []
counter = 0
maxiter = 10
while counter < maxiter:
    counter = counter + 1
    inp = input('Enter a number or finish with [q]: ')
    if inp == 'q':
        break
    try:
        numbers.append(float(inp))
    except:
        print('Invalid input')

print(f'\nProvided numbers: {numbers}')

Enter a number or finish with [q]:  1
Enter a number or finish with [q]:  2
Enter a number or finish with [q]:  3
Enter a number or finish with [q]:  Text
Invalid input
Enter a number or finish with [q]:  q

Provided numbers: [1.0, 2.0, 3.0]

(b) Mutation with side effect:

The following code cell first defines two variables x and y. Then, it prints the sum of y, mutates an element in x, and prints the sum of y again. The two print statements differ.
Make an adjustment to line 2, so that y is not affected by changes in x any more. (2 points)

x = np.arange(10)
y = np.flip(x.copy())  # changes only allowed in this line!

print(y.sum())
x[0] = -9
print(y.sum())

45
45

(c) Functions:

Define a function called approx_sin which implements an approximation of the sine function given by the equation

\[ sin(x) = \sum_{i=0}^n (-1)^i \frac{x^{2i+1}}{(2i+1)!}\]

where \(!\) denotes the number’s factorial and can be computed with the function math.factorial().
The function should take \(x\) and \(n\) as inputs, where \(n\) should default to 5 if not provided by the user.
(3 points)

def approx_sin(x, n=5):
    result = 0
    for i in range(n+1):
        result = result + (-1)**i * x**(2*i+1) / math.factorial(2*i+1)
        
    return result

When you implemented your function, run the following code block to view the approximation error for different \(n\):
(This is not a task anymore, you don’t need to change the code for that!)

x = math.pi / 2
true_value = math.sin(x)
for n in [1, 3, 5, 7]:
    error = abs(approx_sin(x, n) - true_value)
    print(f'Error for x=π/2 and {n=}: {error:e}')

Error for x=π/2 and n=1: 7.516777e-02
Error for x=π/2 and n=3: 1.568986e-04
Error for x=π/2 and n=5: 5.625895e-08
Error for x=π/2 and n=7: 6.023182e-12